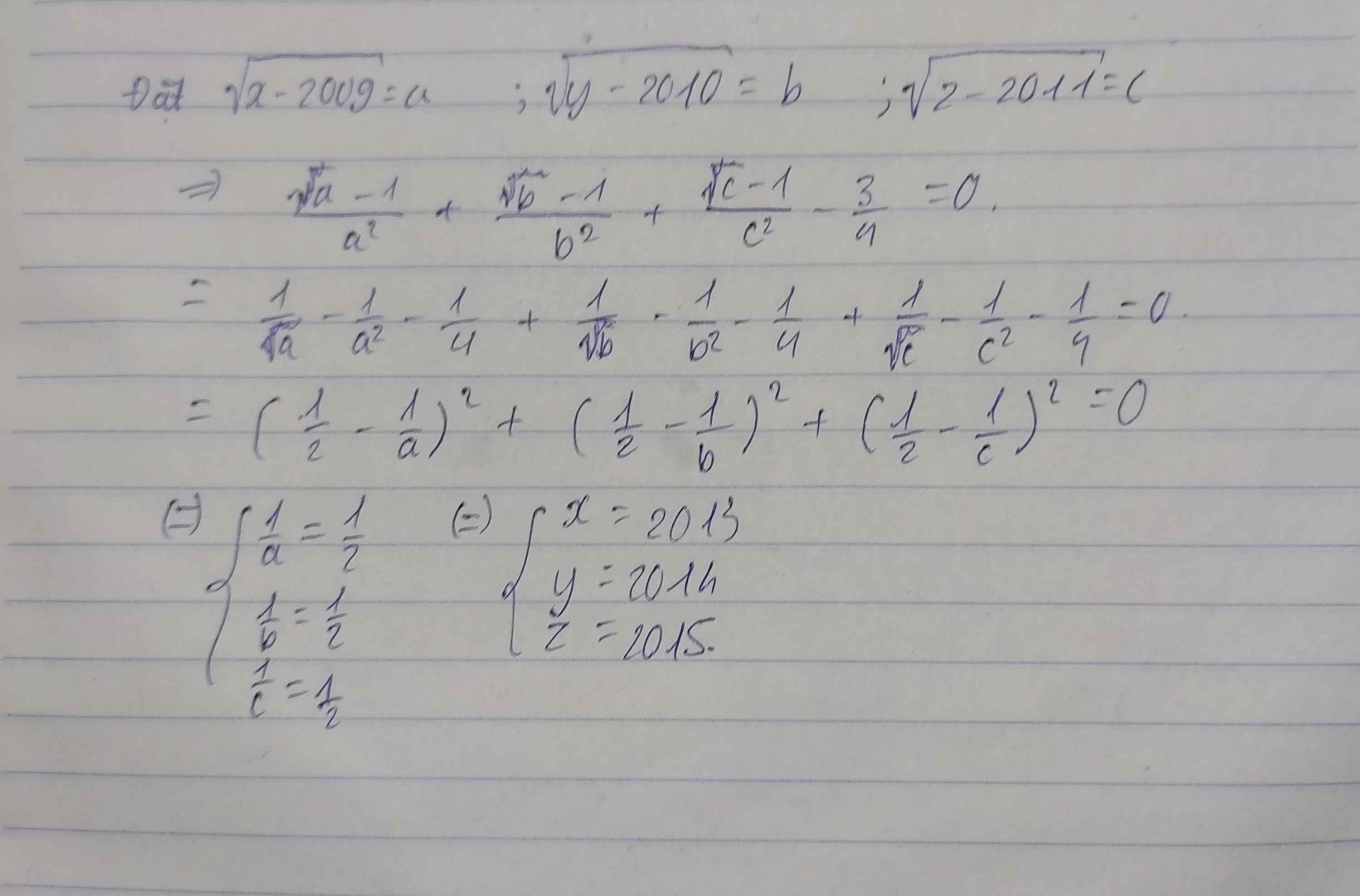10 tháng 6 2022 lúc 20:56
Ôn thi vào 10
Các câu hỏi tương tự
Chứng minh rằng:
\(\dfrac{1}{3\left(\sqrt{2}+1\right)}+\dfrac{1}{5\left(\sqrt{3}+\sqrt{2}\right)}+\dfrac{1}{7\left(\sqrt{4}+\sqrt{3}\right)}+...+\dfrac{1}{4021\left(\sqrt{2011}+\sqrt{2010}\right)}< \dfrac{1}{2}\left(1-\dfrac{1}{\sqrt{2011}}\right)\)
\(\dfrac{\sqrt{x-2015}-1}{x-2015}\) + \(\dfrac{\sqrt{y-2016}-1}{y-2016}\) + \(\dfrac{\sqrt{z-2017}-1}{z-2017}\) = \(\dfrac{3}{4}\)
cho x,y,z là 3 số thực tm \(x+y+z=18\sqrt{2}\).
Cmr \(\dfrac{1}{\sqrt{x\left(y+z\right)}}+\dfrac{1}{\sqrt{y\left(z+x\right)}}+\dfrac{1}{\sqrt{z\left(x+y\right)}}+2\ge\dfrac{9}{4}\)
mng tham khảo
Cho x,y,z dương thỏa mãn \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=3\) . Chứng minh rằng \(\dfrac{1}{\sqrt{2x^2+y^2+3}}+\dfrac{1}{\sqrt{2y^2+z^2+3}}+\dfrac{1}{\sqrt{2z^2+x^2+3}}\) ≤ \(\dfrac{\sqrt{6}}{2}\)
cho các số dương X,Y,Z thỏa mãn :x\(^3\)+Y\(^3\)+Z\(^3\)=1
chứng minh rằng; \(\dfrac{X^2}{\sqrt{1-X^2}}\)+\(\dfrac{Y^2}{\sqrt{1-Y^2}}\)+\(\dfrac{Z^2}{\sqrt{1-Z^2}}\)\(\ge\)2
cho các số thực dương thoả mãn: \(\sqrt{x}+\sqrt{y}+\sqrt{z}=1\)
CMR: \(\sqrt{\dfrac{xy}{x+y+2z}}+\sqrt{\dfrac{yz}{y+z+2x}}\sqrt{\dfrac{zx}{z+x+zy}}\le\dfrac{1}{2}\)
Giải hệ phương trình:
\(\dfrac{1}{3x}+\dfrac{1}{3}\sqrt[]{x+3}=\dfrac{1}{4}x\)
\(\dfrac{5}{6x}+\sqrt[]{y+3}=\dfrac{2}{3}\)
25 tháng 12 2021 lúc 14:54
giải phương trình bằng cách đặt ẩn phụ
a. \(\left\{{}\begin{matrix}\dfrac{2}{x-2}+\dfrac{3}{y-2}=5\\\dfrac{3}{x-2}+\dfrac{2}{y-2}=5\end{matrix}\right.\)
b.\(\left\{{}\begin{matrix}\sqrt{x-3}-2\sqrt{y-1}=2\\2\sqrt{x+3}-\sqrt{y-1}=4\end{matrix}\right.\)
Giải hệ phương trình:
\(\left\{{}\begin{matrix}2\left(\dfrac{x^3}{y^2}+\dfrac{y^3}{x^2}\right)=\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\\16x^5-20x^3+5\sqrt{xy}=\sqrt{\dfrac{y+1}{2}}\end{matrix}\right.\)
Mình đang cần gấp lắm, các bạn giúp mình với. Cảm ơn!
Giải các phương trình sau:
\(a,\dfrac{3}{2}\sqrt{4+12x}-\dfrac{5}{3}\sqrt{9+27x}-\dfrac{1}{4}\sqrt{16+48x}=1\)
\(b,\sqrt{x^2-x+\dfrac{1}{4}}=3\)