1: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=180^0\)
nên AEHF là tứ giác nội tiếp
Xét tứ giác BCEF có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BCEF là tứ giác nội tiếp
2: Xét ΔEHA vuông tại E và ΔECB vuông tại E có
\(\widehat{EAH}=\widehat{EBC}\)
Do đó: ΔEHA\(\sim\)ΔECB
Suy ra: EH/EC=EA/EB
hay \(EA\cdot EC=EH\cdot EB\)















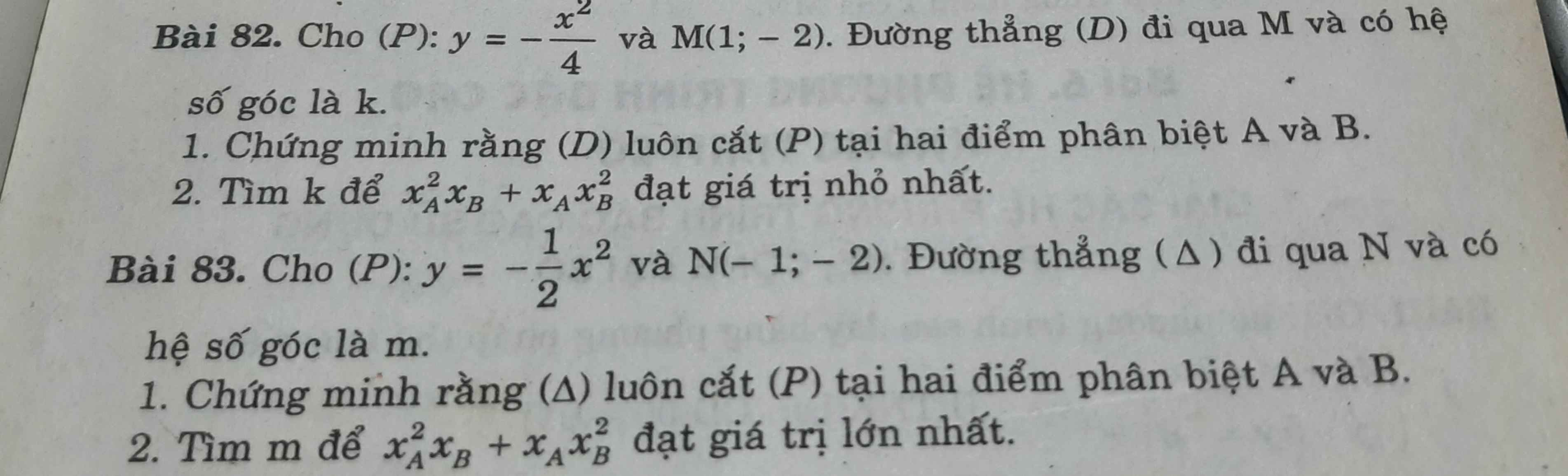



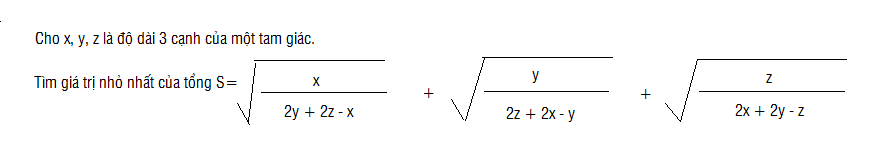


 Giúp mình với ạ , mai mk bộp bài rùi :
Giúp mình với ạ , mai mk bộp bài rùi :