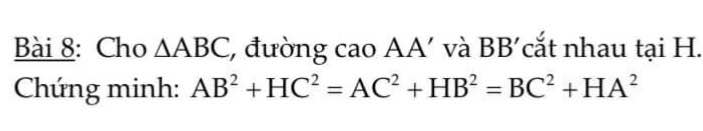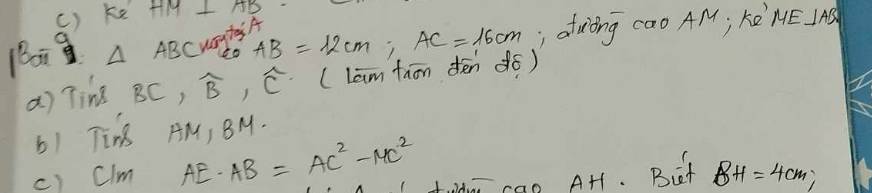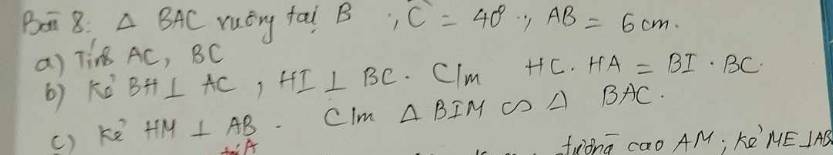Question

 giải giúp

Answer 1

Áp dụng định lý Pitago:

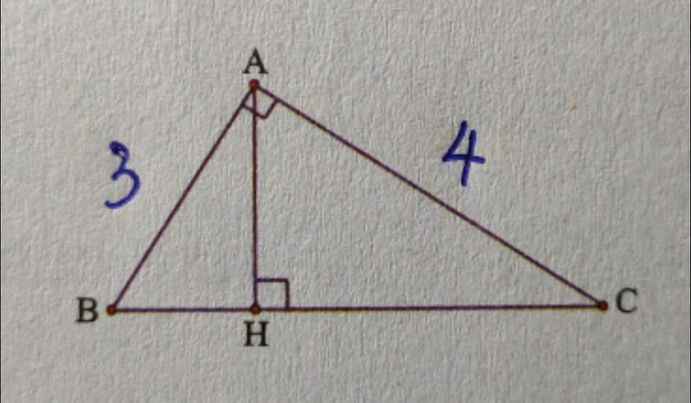
\(BC^2=AB^2+AC^2=3^2+4^2=25\Rightarrow BC=5\)

Áp dụng hệ thức lượng:

\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12}{5}\)

Hệ thức lượng:

\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{9}{5}\)

\(HC=BC-BH=5-\dfrac{9}{5}=\dfrac{16}{5}\)

Answer 2

✱xét △ABC vuông tại A,có:

BC²=AC²+AB²(định lí py-ta-go)

⇒BC=\(\sqrt{AC^2+AB^2}\)

   BC=\(\sqrt{4^2+3^2}\)

   BC=5(cm)

✱xét △ABC vuông tại A,đường cao AH, có:

AB²=BH.BC(hệ thức giữa cạnh và đường cao trong tam giác vuông)

⇒BH=AB²:BC

⇒BH=1,8(cm)

✱BH+CH=BC

⇒CH=BC-BH=5-1,8=3,2(cm)

✱xét △ABC vuông tại A,đường cao AH, có:

CH.BH=AH²(hệ thức giữa cạnh và đường cao trong tam giác vuông)

⇒AH=\(\sqrt{1,8\times3,2}\)= 2,4 (cm)