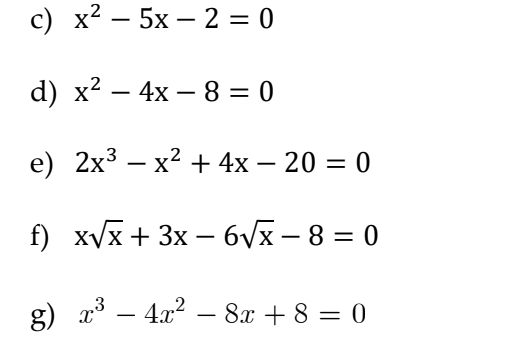c)
\(\Delta=b^2-4ac=\left(-5\right)^2-4.1.-2=33=>\sqrt{\Delta}=\sqrt{33}>0\)
=> pt có 2 nghiệm pb :
\(x_1=\dfrac{-b+\sqrt{33}}{2.1}=\dfrac{5+\sqrt{33}}{2};x_2=\dfrac{5-\sqrt{33}}{2}\)
thí dụ h bn tự lm k bt nào r hỏi đc k:v
c: \(x^2-5x-2=0\)
\(\Delta=\left(-5\right)^2-4\cdot1\cdot\left(-2\right)=25+8=33>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{5-\sqrt{33}}{2}\\x_2=\dfrac{5+\sqrt{33}}{2}\end{matrix}\right.\)
d: \(x^2-4x-8=0\)
\(\Delta=\left(-4\right)^2-4\cdot1\cdot\left(-8\right)=16+32=48>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-4\sqrt{3}}{2}=-2-2\sqrt{3}\\x_2=-2+2\sqrt{3}\end{matrix}\right.\)