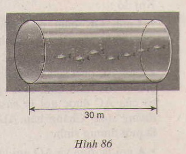
\(V=1.800.000\left(l\right)=1800m^3=S.h\Rightarrow S=\frac{V}{h}=60\left(m^2\right)\)
Chương 2: MẶT NÓN, MẶT TRỤ, MẶT CẦU
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
1)Người ta cần thiết kế một bồn chứa nước có thể tích 400l. Phương án thứ nhất thiết kế theo dạng hình cầu, phương án thứ hai thiết kế theo dạng hình trụ có chiều cao bằng đường kính đáy. Biết cứ mỗi mét vuông nguyên liệu tốn chi phí là 100.000 đồng. Hỏi phương án nào giúp tiết kiệm nguyên liệu hơn và tiết kiệm được bao nhiêu tiền?
1)Cho khối lập phương có độ dài đường chéo bằng sqrt{3}cm. Tính thể tích khối lập phương đó2) Cho hình khối lăng trụ tam giác ABC.ABC có thể tích bằng 1. TÍnh thể tích khối chóp A.ABC theo V3)Cho hình lăng trụ đứng ABC.ABC có đáy là tamiacs đều cạnh a và đường thẳng AC tạo với mặt phẳng (ABBA) một góc 300 . Tính thể tích khối lăng trụ ABC.ABC4)Cho hình chóp tam giác S.ABC có ASBCSB600 , SASBSC2a. Tính thể tích khối chóp S.ABCD5) Cho hình chóp S.ABCD có SA vuông góc với (ABCD), SBasqrt{5}, ABCD l...
Đọc tiếp
1)Cho khối lập phương có độ dài đường chéo bằng \(\sqrt{3}\)cm. Tính thể tích khối lập phương đó
2) Cho hình khối lăng trụ tam giác ABC.A'B'C' có thể tích bằng 1. TÍnh thể tích khối chóp A'.ABC' theo V
3)Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tamiacs đều cạnh a và đường thẳng A'C tạo với mặt phẳng (ABB'A') một góc 300 . Tính thể tích khối lăng trụ ABC.A'B'C'
4)Cho hình chóp tam giác S.ABC có ASB=CSB=600 , SA=SB=SC=2a. Tính thể tích khối chóp S.ABCD
5) Cho hình chóp S.ABCD có SA vuông góc với (ABCD), SB=\(a\sqrt{5}\), ABCD là hình thoi cạnh a, góc ABC = 600 . Tính thể tích khối chóp S.ABCD
Có một quả bóng hình cầu đặc đường kính 20cm được đặt đứng yên trên mặt phẳng nằm ngang. Người ta lấy một chiếc nón úp vào quả bóng thì thấy đáy nón vừa chạm với mặt phẳng nằm ngang và các đường sinh của mặt nón cũng vừa tiếp xúc với bề mặt của quả bóng. Biết rằng độ rộng của góc ở đỉnh nón là 60^0. Tính thể tích của khối nón giới hạn bởi chiếc nón và mặt phẳng nằm ngang và tính phần không gian bên trong khối nón mà không bị quả bóng chiếm chỗ
Đọc tiếp
Có một quả bóng hình cầu đặc đường kính 20cm được đặt đứng yên trên mặt phẳng nằm ngang. Người ta lấy một chiếc nón úp vào quả bóng thì thấy đáy nón vừa chạm với mặt phẳng nằm ngang và các đường sinh của mặt nón cũng vừa tiếp xúc với bề mặt của quả bóng. Biết rằng độ rộng của góc ở đỉnh nón là \(60^0\). Tính thể tích của khối nón giới hạn bởi chiếc nón và mặt phẳng nằm ngang và tính phần không gian bên trong khối nón mà không bị quả bóng chiếm chỗ
Khối hộp ABCDA'B'C'D' có đáy là hình chữ nhật với AB=\(\sqrt{3}\) ; AD=\(\sqrt{7}\) . Các đường chéo AC' và DB' lần lượt tao với đáy các góc 45 hoặc 60, chiều cao của nó bằng 2, tính thể tích lăng trụ.
A.2B.4C.3D.1cho hình nón có bán kính đáy R, góc giữa đường sinh và đáy của hình nón là anpha. một mặt phẳng (P) sog song với đáy của hình nón, cách đáy hình nón một khoảng h, cắt hình nón theo đường tròn (C). tính bán kính đtron (C) theo R,h và anpha
Giúp vs t đang cần gấp ạ: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC có đáy ABC là tam giác vuông cân tại B; AB a, góc ACB 30 độ, M là trung điểm cạnh AC. Góc giữa cạnh bên và mặt đáy của lăng trụ bằng 60 độ. Hình chiếu vuông góc của đỉnh A’ lên mặt phẳng (ABC) là trung điểm H của BM. Tính theo a thể tích khối lăng trụ ABC.A’B’C’và khoảng cách từ điểm C’ đến mặt phẳng (BMB’).
Đọc tiếp
Giúp vs t đang cần gấp ạ: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC có đáy ABC là tam giác vuông cân tại B; AB = a, góc ACB = 30 độ, M là trung điểm cạnh AC. Góc giữa cạnh bên và mặt đáy của lăng trụ bằng 60 độ. Hình chiếu vuông góc của đỉnh A’ lên mặt phẳng (ABC) là trung điểm H của BM. Tính theo a thể tích khối lăng trụ ABC.A’B’C’và khoảng cách từ điểm C’ đến mặt phẳng (BMB’).
Trong không gian cho hình chữ nhật ABCD có AB=1, AD=2. Gọi M,N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần của hình trụ đó.
Trong không gian cho hình chữ nhật ABCD có AB=1, AD=2. Gọi M,N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần của hình trụ đó.
Cho hình chóp S. ABCD, có đáy hình thang vuông góc tại A và B, AB = BC =a căn3. AD = 2BC, đường thẳng SA vuông góc vs mặt phẳng (ABCD) đg thẳng SC tạo với mp (ABCD) một góc bằng 60đ, gọi E là trung điểm của cạnh SC, tính theo a a) tính thể tích của khối chóp S.ABCD. b) tính thể tích của khối tứ diện EACD. c) kcách từ điểm E đến mp SAD
Xem chi tiết