Có công thức:
`100*(1+x/100)^3=119,1016`
`<=>1+x/100=1,06`
`<=>x/100=0,06`
`<=>x=6`
Đề bài
Dân số được ước tính theo công thức \(S = A.{e^{r.t}}\), trong đó A là dân số của năm lấy làm mốc tính, S là dân số sau t năm, r là tỉ lệ tăng dân số hàng năm. Hỏi sau bao nhiêu năm, dân số sẽ gấp đôi dân số của năm lấy làm mốc tính?
Hoạt động 6
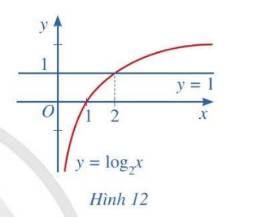
Quan sát Hình 12 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số lôgarit \(y = {\log _2}x\). Từ đó, hãy tìm x sao cho \({\log _2}x > 1\)
Hoạt động 5
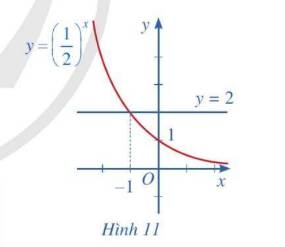
Quan sát Hình 11 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số mũ \(y = {\left( {\frac{1}{2}} \right)^x}\). Từ đó, hãy tìm x sao cho \({\left( {\frac{1}{2}} \right)^x} > 2\)
Đề bài
Sử dụng công thức tính mức cường độ âm L ở Ví dụ 14, hãy tính mức cường độ âm mà tai người có thể nghe được, biết rằng tai người có thể nghe được âm với cường độ âm từ \({10^{ - 12}}W/{m^2} \to 10W/{m^2}\)
Hoạt động 1
Trong bài toán ở phần mở đầu, giả sử
a) Viết phương trình thể hiện dân số sau t năm gấp đôi dân số ban đầu
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lũy thừa?
Chỉ số hay độ pH của một dung dịch được tính theo công thức: \(pH = - \log [{H^ + }]\) (Trong đó \([{H^ + }]\) chỉ nống độ hydrogen). Đo chỉ số pH của một mẫu nước sông, ta có kết quả là pH = 6,1.
a) Viết phương trình thể hiện nồng độ x của ion hydrogen \([{H^ + }]\) trong mẫu nước sông đó.
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lôgarit?
a) Vẽ đồ thị hàm số \(y = {3^x}\) và đường thẳng y = 7
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình \({3^x} = 7\)
a) Vẽ đồ thị hàm số \(y = {\log _4}x\) và đường thẳng y = 5
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình \({\log _4}x = 5\)
Đề bài
Giải mỗi bất phương trình sau:
a) \({3^x} > \frac{1}{{243}}\)
b) \({\left( {\frac{2}{3}} \right)^{3x - 7}} \le \frac{3}{2}\)
c) \({4^{x + 3}} \ge {32^x}\)
d) \(\log (x - 1) < 0\)
e) \({\log _{\frac{1}{5}}}(2x - 1) \ge {\log _{\frac{1}{5}}}(x + 3)\)
f) \(\ln (x + 3) \ge \ln (2x - 8)\)
