Đề bài
Dân số được ước tính theo công thức \(S = A.{e^{r.t}}\), trong đó A là dân số của năm lấy làm mốc tính, S là dân số sau t năm, r là tỉ lệ tăng dân số hàng năm. Hỏi sau bao nhiêu năm, dân số sẽ gấp đôi dân số của năm lấy làm mốc tính?
Bài 4. Phương trình mũ, bất phương trình mũ và lôgarit
Giải hoạt động mở đầu trang 48 (SGK Cánh Diều)
Thảo luận (1)
Hoạt động 1,Giải mục 1 trang 48, 49, 50 (SGK Cánh Diều)
Hoạt động 1
Trong bài toán ở phần mở đầu, giả sử
a) Viết phương trình thể hiện dân số sau t năm gấp đôi dân số ban đầu
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lũy thừa?
Thảo luận (1)Hướng dẫn giảia) Phương trình thể hiện dân số sau t năm gấp đôi dân số ban đầu là:
\(S=2S.e^{1,14.t}\Leftrightarrow2e^{1,14t}=1\Leftrightarrow e^{1,14t}=\dfrac{1}{2}\)
b) Phương trình vừa tìm được có ẩn là t và nằm ở vị trí mũ của lũy thừa
(Trả lời bởi Mai Trung Hải Phong)
Luyện tập – Vận dụng 1,Giải mục 1 trang 48, 49, 50 (SGK Cánh Diều)
Cho hai ví dụ về phương trình mũ
Thảo luận (2)Hướng dẫn giải
Hoạt động 2,Giải mục 1 trang 48, 49, 50 (SGK Cánh Diều)
a) Vẽ đồ thị hàm số \(y = {3^x}\) và đường thẳng y = 7
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình \({3^x} = 7\)
Thảo luận (1)Hướng dẫn giảiTa có bảng sau:
Ta có đồ thị sau:
b, Hai đồ thị \(y=3^x\) và \(y=7\) có \(1\) giao điểm. Vậy số nghiệm của phương trình \(3^x=7\) là \(1\)
(Trả lời bởi Mai Trung Hải Phong)
Luyện tập – Vận dụng 2,Giải mục 1 trang 48, 49, 50 (SGK Cánh Diều)
Giải mỗi phương trình sau:
a) \({9^{16 - x}} = {27^{x + 4}}\)
b) \({16^{x - 2}} = 0,{25.2^{ - x + 4}}\)
Thảo luận (1)Hướng dẫn giảia)
\(9^{16-x}=27^{x+4}\\ \Leftrightarrow3^{2.\left(16-x\right)}=3^{3.\left(x+4\right)}\\ \Leftrightarrow2.\left(16-x\right)=3.\left(x+4\right)\\ \Leftrightarrow32-2x-3x-12=0\\ \Leftrightarrow-5x=-20\Leftrightarrow x=4\)
b)
\(16^{x-2}=0,25.2^{-x+4}\\ \Leftrightarrow2^{4\left(x-2\right)}=0,25.2^{-x+4}\\ \Leftrightarrow2^{4x-8+x-4}=0,25\\ \Leftrightarrow2^{5x-12}=0,25\Leftrightarrow5x-12=\log_20,25\\ \Leftrightarrow5x-12=-2\\ \Leftrightarrow x=2\)
(Trả lời bởi Mai Trung Hải Phong)
Hoạt động 3,Giải mục 1 trang 48, 49, 50 (SGK Cánh Diều)
Chỉ số hay độ pH của một dung dịch được tính theo công thức: pH - log [{H^ + }] (Trong đó [{H^ + }] chỉ nống độ hydrogen). Đo chỉ số pH của một mẫu nước sông, ta có kết quả là pH 6,1.a) Viết phương trình thể hiện nồng độ x của ion hydrogen [{H^ + }] trong mẫu nước sông đó.b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lôgarit?
Đọc tiếp
Chỉ số hay độ pH của một dung dịch được tính theo công thức: \(pH = - \log [{H^ + }]\) (Trong đó \([{H^ + }]\) chỉ nống độ hydrogen). Đo chỉ số pH của một mẫu nước sông, ta có kết quả là pH = 6,1.
a) Viết phương trình thể hiện nồng độ x của ion hydrogen \([{H^ + }]\) trong mẫu nước sông đó.
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lôgarit?
Thảo luận (1)Hướng dẫn giảia) Ta có:\(-\log\left[H^+\right]=6.1\Leftrightarrow-\log x=6,1\)
b) Phương trình vừa tìm được có ẩn là x và nằm ở vị trí hệ số của logarit
(Trả lời bởi Mai Trung Hải Phong)
Luyện tập – Vận dụng 3,Giải mục 1 trang 48, 49, 50 (SGK Cánh Diều)
Cho hai ví dụ về phương trình logarit
Thảo luận (2)Hướng dẫn giải
Hoạt động 4,Giải mục 1 trang 48, 49, 50 (SGK Cánh Diều)
a) Vẽ đồ thị hàm số \(y = {\log _4}x\) và đường thẳng y = 5
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình \({\log _4}x = 5\)
Thảo luận (1)Hướng dẫn giảia:
b: Hai đồ thị này có 1 giao điểm
=>Phương trình \(log_4x=5\) có 1 nghiệm duy nhất
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Luyện tập – Vận dụng 4,Giải mục 1 trang 48, 49, 50 (SGK Cánh Diều)
Giải mỗi phương trình sau:
a) \({\log _5}\left( {2x - 4} \right) + {\log _{\frac{1}{5}}}\left( {x - 1} \right) = 0\)
b) \({\log _2}x + {\log _4}x = 3\)
Thảo luận (1)Hướng dẫn giảia)
ĐK: \(\left\{{}\begin{matrix}2x-4>0\\x-1>0\end{matrix}\right.\Leftrightarrow x>1\)
\(\log_5\left(2x-4\right)+\log_{\dfrac{1}{5}}\left(x-1\right)=0\\ \Leftrightarrow\log_5\left(2x-4\right)-\log_5\left(x-1\right)=0\\ \Leftrightarrow\log_5\left(\dfrac{2x-4}{x-1}\right)=\log_51\\ \Leftrightarrow\dfrac{2x-4}{x-1}=1\\ \Leftrightarrow2x-4=x-1\\ \Leftrightarrow x=3\left(tm\right)\)
Vậy x = 3.
b) ĐK: x > 0
\(\log_2x+\log_4x=3\\ \Leftrightarrow\log_2x+\dfrac{1}{2}\log_2x=3\\ \Leftrightarrow\left(1+\dfrac{1}{2}\right)\log_2x=3\\ \Leftrightarrow\dfrac{3}{2}\log_2x=3\\ \Leftrightarrow\log_2x=2\\ \Leftrightarrow x=4\left(tm\right)\)
Vậy x= 4
(Trả lời bởi datcoder)
Giải mục 2 trang 51, 52, 53,Hoạt động 5 (SGK Cánh Diều)
Hoạt động 5
Quan sát Hình 11 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số mũ \(y = {\left( {\frac{1}{2}} \right)^x}\). Từ đó, hãy tìm x sao cho \({\left( {\frac{1}{2}} \right)^x} > 2\)
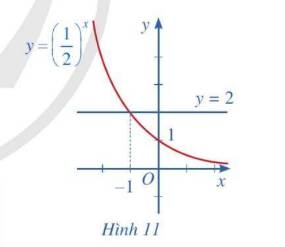
Thảo luận (1)Hướng dẫn giảiDo \(\dfrac{1}{2}< 1\) ⇒ Hàm số \(y=\left(\dfrac{1}{2}\right)^x\) nghịch biến trên R.
\(\left(\dfrac{1}{2}\right)^x>2\\ \Rightarrow x< log_{\dfrac{1}{2}}2\\ \Rightarrow x< -1\)
(Trả lời bởi Hà Quang Minh)