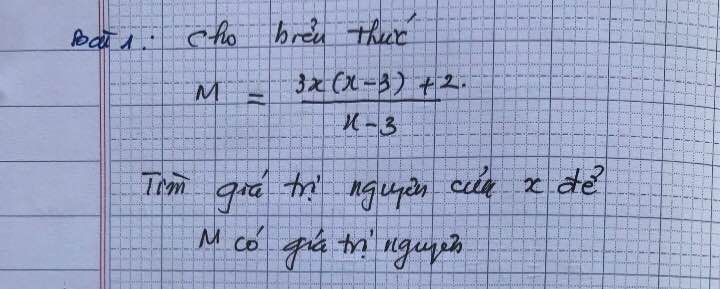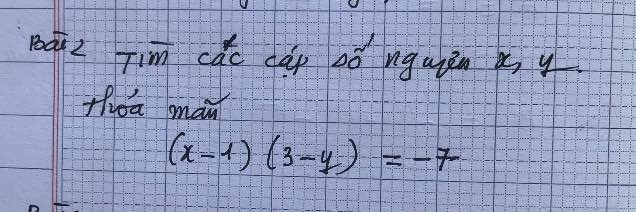Question

Đang cần gấp nếu làm nhanh và chính xác chi tiết sẽ có tick nhanh

Answer 1

\(M=\dfrac{3x\left(x-3\right)+2}{x-3}\)

\(\Rightarrow M=\dfrac{3x\left(x-3\right)}{x-3}+\dfrac{2}{x-3}\)

\(\Rightarrow M=3x+\dfrac{2}{x-3}\)

Để M nguyên thì \(\dfrac{2}{x-3}\in Z\Rightarrow x-3\inƯ\left(2\right)=\left\{\pm1;\pm3\right\}\)

Ta có bảng:

x-3	-1	-3	1	3
x	2	0	4	6

Vậy \(x\in\left\{2;0;4;6\right\}\)