Chương 1: PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG TRONG MẶT PHẲNG
Các câu hỏi tương tự
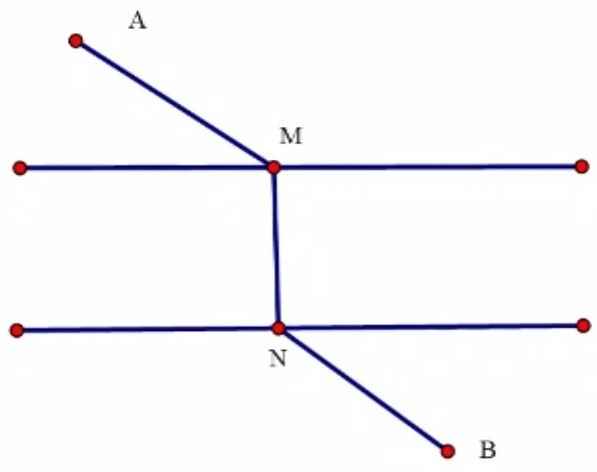
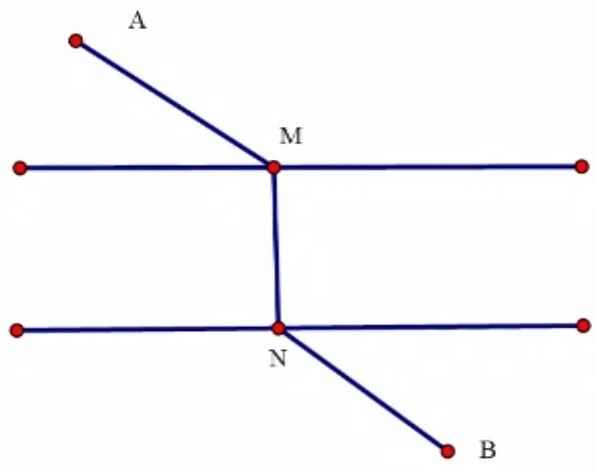
Tìm vị trí M, N để tổng khoảng cách: AM + MN + NB nhỏ nhất?
Tam giác ABC cân tại A. M là điểm bất kì trên BC. CMR: Tổng khoảng cách từ M đến cạnh AB và AC không đổi ( tức không phụ thuộc vào vị trí của M )
2. Cho \(\Delta ABC\) có trọng tâm G và nội tiếp trong đường tròn (O) B, C cố định. Dựng hình bình hành BGCD. Tìm quỹ tích điểm D khi A thay đổi trên (O)
Cho hình vuông ABCD có tâm O. Biết tâm O cố định và A là điểm thay đổi luôn thuộc đường thẳng đenta cố định. Tìm quỹ tích điểm B.
cho tam giác ABC có ABC có A cố định. Hai điểm B,C thay đổi sao cho AB=2, AC=5. Dựng tam giác đều BCD sao cho D khác phía với A đối với BC. Xác định góc BAC để AD có độ dài lớn nhất
Cho hai điểm A, B và đường tròn tâm O không có điểm chung với đường thẳng AB.
a. Dựng ảnh (O') là ảnh của (O) qua phép tịnh tiến theo véc tơ AB
b. Cho M di động trên (O) dựng hình bình hành MABN. CMR: Điểm N chạy trên đường tròn cố định khi M thay đổi.
A-C-B-D-D-C-B-C
Trong mặt phẳng tọa độ Oxy cho đường thẳng d: x - 2y + 2 = 0 và A(0;6), B(2;5). Tìm tọa độ điểm M trên đường thẳng d sao cho MA + MB nhỏ nhất
Cho hình thang ABCD có hai dáy AB = 15cm,CD = 60cm. Xác định một phép vị tụ biển đoạn thẳng AB thành đoạn thẳng CD.
1. Cho đường tròn (O;R) và 1 điểm A cố định trên đường tròn, BC là 1 dây cung di động của đường tròn này và BC có độ dài không đổi = 2d (d<R). Tìm tập hợp trọng tâm G của \(\Delta ABC\)