\(x^2+2x+3>0\\ \Leftrightarrow\left(x^2+2x+1\right)+2>0\\ \Leftrightarrow\left(x+1\right)^2+2>0\left(luôn.đúng\forall x\in R\right)\)
Vậy \(\forall x\in R\) thì \(x^2+2x+3>0\)
x^2 +2x+3>0
<=> (x^2 +2x +1) +2 >0
<=>(x+1)^2 +2>0( luôn đúng)
\(x^2+2x+3>0\\ \Leftrightarrow\left(x^2+2x+1\right)+2>0\\ \Leftrightarrow\left(x+1\right)^2+2>0\left(luôn.đúng\forall x\in R\right)\)
Vậy \(\forall x\in R\) thì \(x^2+2x+3>0\)
x^2 +2x+3>0
<=> (x^2 +2x +1) +2 >0
<=>(x+1)^2 +2>0( luôn đúng)
Chứng minh:
Chứng minh rằng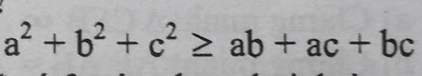
2x^2-6x+1=0 ( giải phương trình tích)
a) chứng minh -x^2+4x-9<=-5
b) chứng minh x^2-2x+9>= với mọi số thực x
Giup minh voi .mai kt roi
Chứng minh
(x+y)^2>=4xy
chứng minh rằng : nếu a > b thì 2a > 2b - 1
chứng minh x^4+16>=2x^3+8x
Chứng minh: a^2+b^2-a-b >= 0
Cho \(x_1,x_2\in\left[0,1\right]\)
a) Chứng minh \(\left(1+x_1\right)^2\ge4x_1^2\)
b) Chứng minh \(\left(1+x_1+x_2\right)^2\ge4\left(x_1^2+x_2^2\right)\)
1/Cho (a2 - bc)( b- abc) = (b2 -ac)(a-abc)
a/ Chứng minh rằng: 1/a + 1/b + 1/c = a+b+c
b/ Chứng tỏ : a(b-c)(b+c-a)2 + c(a-b)(a+b-c)2 = b(a-c)(a+c-b)
2/ Với x là 1 số thực bất kỳ. Chứng minh rằng x-x2 +1: x2 -1 <1
3/ Cho các số x,y thỏa mãn : Chứng minh rằng x2 +y2 +(1+xy : x+y)2 >=2