Ôn tập chương II - Đa giác. Diện tích đa giác
Các câu hỏi tương tự
Cho tam giác ABC. Gọi M, N là các trung điểm tương ứng của AC, BC. Chứng minh rằng diện tích của hình thang ABNM bằng \(\dfrac{3}{4}\) diện tích của tam giác ABC ?
Gọi O là điểm nằm trong hình bình hành ABCD. Chứng minh rằng tổng diện tích của hai tam giác ABO và CDO bằng tổng diện tích của hai tam giác BCO và DAO ?
cho hình thang abcd có ab=5cm cd=15cm ac=16 bd=12cm từ a vẽ đường thằng song song vs bd cắt cd tại e A,chứng minh rằng tam giác ace là tam giác vuông B, tính diện tích của tứ giác abcd
Bài 2: Cho hình bình hành ABCD có CD = 16 cm, đường cao vẽ từ A đến cạnh CD bằng 12 cm. \
a,Tính diện tích hình bình hành ABCD.
b,Gọi M là trung điểm AB, Tính diện tích tam giác ADM.
c,DM cắt AC tại N. Chứng minh rằng DN= 2NM
d, Tính diện tích tam giác AMN.
Cho hình thang ABCD ( AB//CD, AB<CD).Qua M là trung điểm BC, kẻ đường thẳng // AD cắt CD ở E,cắt AB ở F
a) C/m AFED là hbh
b) C/m BFCE là hbh
c) C/m diện tích tam giác ADE= dtich tam giác BEC= 1/2 diện tích ABCD
Cho tam giác ABC vuông ở A và có BC = 2 AB = 2a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều ACG
a) Tính các góc B, C cạnh AC và diện tích tam giác ABC
b) Chứng minh rằng FA vuông góc với BE và CG. Tính diện tích các tam giác FAG và FBE
c) Tính diện tích tứ giác DEFG
Cho hình bs.31
(R là điểm bất kì trên QP. S là điểm bất kì trên NO, hình thang NOPQ có diện tích S). Khi đó, tổng diện tích của hai tam giác QSP và NRO bằng :
(A) dfrac{1}{2}S (B) dfrac{1}{4}S
(C) dfrac{3}{4}S (D) S
Hãy lựa chọn phương án đúng ?
Đọc tiếp
Cho hình bs.31
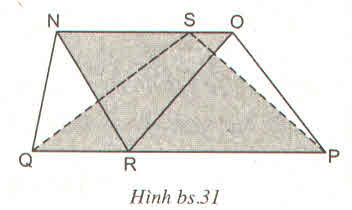
(R là điểm bất kì trên QP. S là điểm bất kì trên NO, hình thang NOPQ có diện tích S). Khi đó, tổng diện tích của hai tam giác QSP và NRO bằng :
(A) \(\dfrac{1}{2}S\) (B) \(\dfrac{1}{4}S\)
(C) \(\dfrac{3}{4}S\) (D) \(S\)
Hãy lựa chọn phương án đúng ?
Cho hình thang NPQM (MN//QP).X là điểm thuộc MN, Y là điểm thuộc PQ . Chứng minh rằng diện tích hình thang MNPQ bằng tổng diện tích hai tam giác XPQ và YMN
Cho hình thang NPQM (MN//QP).X là điểm thuộc MN, Y là điểm thuộc PQ . Chứng minh rằng diện tích hình thang MNPQ bằng tổng diện tích hai tam giác XPQ và YMN







