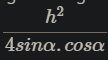Chương I - Hệ thức lượng trong tam giác vuông
Các câu hỏi tương tự
Bài 4.Cho hình thoi ABCD có A= 120 độ, tia Ax tạo với tia AB góc BAx =15 độ, cắt BC, CD lần lượt tại M, N. Chứng minh: 1/AM mũ 2 + 1/AN mũ 2= 1/3AB mũ 2
Cho hình thang ABCD có góc B= góc C =90o. Hai đường chéo vuông góc với nhau tại H. Biết AB=3 căn 5 cm,HA=3cm. Chứng minh
HA:HB:HC:HD=1:2:4:8
Help me,please
7, cho tg ABC vg tại A và góc B=30 độ, BC= 12cm. Tính độ dài 2 cạnh còn lại và độ dài đg cao AH của tg đó
cho tg ABC có AB=1 ∠A = 105 độ , ∠B=60 độ, trên cạnh BC lấy điểm E sao cho BE=1 , vẽ ED // AB ( DϵAC) . c/m\(\frac{1}{AC^2}+\frac{1}{AD^2}=\frac{4}{3}\)
cho biểu thức B = ( căn x - 2 phần x-1 - căn x + 2 phần x+2 căn x +1) . (1-x)2 phần 2
a/ tìm điều kiện xác đinh và rút gọn B
b/ chứng tỏ rằng nếu 0<x<1 thì B>0
c/tính giá trị lớn nhất của B
đg pg thuộc cạnh huyền chia c huyền của tg vg ABC(vg ở A) thành 2 đoạn thẳng theo tỉ số 3/4. tính độ dài của 2 cgv AB và AC bt cạnh huyền BC=10cm
4, cho tg ABC cân tại A, đường cao ứng vs cạnh bên có độ dài bằng h, góc ở đáy của tg bằng α. CMR: \(S^{_{ABC}}=\dfrac{h^2}{4sin\alpha.cos\alpha}\)
Cho tam giác ABC có ba góc nhọn và ABAC. Vẽ hai đường cao BD và CE. 1.Chứng minh : tam giác ABD đồng dạng tam giác ACE 2.Chứng minh: tam giác ADE đồng dạng tam giác ABC 3.Tia DE và CB cắt nhau tại I. Chứng minh : tam giác IDE đồng dạng tam giác IDC 4.Gọi O là trung điểm của BC. Chứng minh : ID.IEOI^2 - OC^2
Đọc tiếp
Cho tam giác ABC có ba góc nhọn và AB<AC. Vẽ hai đường cao BD và CE. 1.Chứng minh : tam giác ABD đồng dạng tam giác ACE 2.Chứng minh: tam giác ADE đồng dạng tam giác ABC 3.Tia DE và CB cắt nhau tại I. Chứng minh : tam giác IDE đồng dạng tam giác IDC 4.Gọi O là trung điểm của BC. Chứng minh : ID.IE=OI^2 - OC^2
4, cho tg ABC cân tại A, đường cao ứng vs cạnh bên có độ dài bằng h, góc ở đáy của tg bằng α. CMR:SABC=