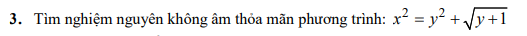a/ Do 1998 là số chẵn \(\Rightarrow\) x và y cùng chẵn hoặc cùng lẻ
TH1: x và y cùng chẵn \(\Rightarrow\left\{{}\begin{matrix}x=2m\\y=2n\end{matrix}\right.\)
\(\Rightarrow VT=\left(2m\right)^2-\left(2n\right)^2=4\left(m^2-n^2\right)⋮4\)
\(VP=1998⋮̸4\)
Phương trình vô nghiệm
TH2: x và y cùng lẻ \(\Rightarrow\left\{{}\begin{matrix}x=2m+1\\y=2n+1\end{matrix}\right.\)
\(VT=\left(2m+1\right)^2-\left(2n+1\right)^2=4\left(m^2+m-n^2-n\right)⋮4\)
Vế phái vẫn ko chia hết cho 4 nên pt vô nghiệm
Vậy ko có x; y nguyên thỏa mãn hay pt ko có nghiệm nguyên
b.
Đề bài sai
Phản ví dụ: với \(\left(x;y\right)=\left(25;37\right)\) là 1 cặp nghiệm nguyên của pt