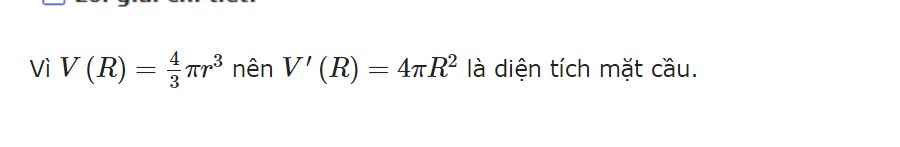Bài 2: Quy tắc tính đạo hàm
Các câu hỏi tương tự
Giả sử V là thể tích hình trụ tròn xoay với chiều cao h và bán kính đáy r. Chứng minh rằng với r là hằng số thì đạo hàm V'(h) bằng diện tích đáy hình trụ và với h là hằng số thì đạo hàm V'(r) bằng diện tích xung quanh của hình trụ ?
Chứng minh rằng nếu \(S\left(r\right)\) là diện tích hình tròn bán kính r thì \(S'\left(r\right)\) là chu vi đường tròn đó ?
cho các ham số f(x), g(x) có đạo hàm trên r và thỏa mãn f(x+3)=g(x) + \(x^2\) - 10x +5 với mọi x thuộc R, f'(4)=5. Tính g'(1)
Cho hàm số y=f(x) có đạo hàm trên R và thỏa mãn f(1+3x)=2x-f(1-2x) với mọi \(x\in R\) . Lập phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x=1 .
1. Cho hàm số yx^3-3mx^2+3left(2m-1right)x+1 . Với giá trị nào của m thì fleft(xright)-6x0 với mọi x2A. m 1/2 B. m -1/2 C. m 1 D. m ≤ 02. Cho hai hàm số f(x) và g(x) đều có đạo hàm trên R và thỏa mãn : f^3left(2-xright)-2f^2left(2+3xright)+x^2gleft(xright)+36x0 với mọi x thuộc R.Tính A3fleft(2right)+4fleft(2right)3. Biết hàm số f(x) - f(2x) có đạo hàm bằng 18 tại x1 và đạo hàm bằng 2000 tại x2. Tính đạo hàm của hàm số f(x) - f(4x) tại x1
Đọc tiếp
1. Cho hàm số \(y=x^3-3mx^2+3\left(2m-1\right)x+1\) . Với giá trị nào của m thì \(f'\left(x\right)-6x>0\) với mọi x>2
A. m > 1/2 B. m < -1/2 C. m >1 D. m ≤ 0
2. Cho hai hàm số f(x) và g(x) đều có đạo hàm trên R và thỏa mãn :
\(f^3\left(2-x\right)-2f^2\left(2+3x\right)+x^2g\left(x\right)+36x=0\) với mọi x thuộc R.
Tính \(A=3f\left(2\right)+4f'\left(2\right)\)
3. Biết hàm số f(x) - f(2x) có đạo hàm bằng 18 tại x=1 và đạo hàm bằng 2000 tại x=2. Tính đạo hàm của hàm số f(x) - f(4x) tại x=1
bài 1: cho hàm số y 2x3 - 3(2m+1)x2 + 6m(m+1)x + 1. Chứng minh rằng y 0 luôn có hai nghiệm phân biệt với x2 - x1 không phụ thuộc vào m.
bài 2: cho hàm số y [(m-1)x3]/3 + mx2 + (3m-2)x. tìm m để y ≥ 0 với mọi x thuộc R
bài 3: cho hàm số y [x2 + (m-1)x + 2 ]/(x-1). tìm m để y 0 có hai nghiệm thỏa mãn x1.x2 -3
bài 4: cho hàm số y (x2+ mx - 1)/(x-1) tìm m để y ≥ 0 với mọi x ≠ 1.
bài 5: cho hàm số y mx3 + 3mx2 - (m-1)x - 1. tìm m để y 0 không có hai nghiệm phân biệt.
Đọc tiếp
bài 1: cho hàm số y = 2x3 - 3(2m+1)x2 + 6m(m+1)x + 1. Chứng minh rằng y' = 0 luôn có hai nghiệm phân biệt với x2 - x1 không phụ thuộc vào m.
bài 2: cho hàm số y = [(m-1)x3]/3 + mx2 + (3m-2)x. tìm m để y' ≥ 0 với mọi x thuộc R
bài 3: cho hàm số y = [x2 + (m-1)x + 2 ]/(x-1). tìm m để y' = 0 có hai nghiệm thỏa mãn x1.x2 = -3
bài 4: cho hàm số y = (x2+ mx - 1)/(x-1) tìm m để y' ≥ 0 với mọi x ≠ 1.
bài 5: cho hàm số y = mx3 + 3mx2 - (m-1)x - 1. tìm m để y' = 0 không có hai nghiệm phân biệt.
y=f(x) xác định có đạo hàm trên R thỏa mãn : \(\left[f\left(1+2x\right)\right]^2=x-\left[f\left(1-x\right)\right]^3\) . Viết phương trình tiếp tuyến tại điểm có hoành độ x =1 .
cho hàm số f(x)= x3+(a-1)x2+2x+1. để f '(x) >0,với mọi x thuộc R nếu:
a. 1-\(\sqrt{6}\le a\le1+\sqrt{6}\) b. \(1-\sqrt{6}< a< 1+\sqrt{6}\)
c. \(a< 1+\sqrt{6}\) d. \(a\ge1-\sqrt{6}\)
mk cần giải chi tiết ạ( đang cần gấp)
help my! thank nhìu <3 !!!
Xác định m để bất phương trình sau nghiệm đúng với mọi \(x\in R\)
a) \(f'\left(x\right)>0\) với \(f\left(x\right)=\dfrac{m}{3}x^3-3x^2+mx-5\)
b) \(g'\left(x\right)< 0\) với \(g\left(x\right)=\dfrac{m}{3}x^3-\dfrac{m}{2}x^2+\left(m+1\right)x-15\)