§2. Bất phương trình và hệ bất phương trình một ẩn
Các câu hỏi tương tự
Cho a,b,c > 0 và a2 +b2+c2 = 1. Chứng minh rằng :\(\dfrac{a}{b^2+c^2}+\dfrac{b}{c^2+a^2}+\dfrac{c}{a^2+b^2}\ge\dfrac{3\sqrt{3}}{2}\)
Bài 14 : Cho \(\Delta ABC\) tìm : \(\sin^2A=\sin B.\sin C\) chứng minh rằng
a , \(a^2=bc\)
b , \(\cos A\ge\frac{1}{2}\)
Cho phương trình :\(x^2-2mx+2m-1=0\)
a , chứng minh phương trình có nghiệm với mọi m
b , Tìm m để phương trình có 1 nghiệm gấp đôi nghiệm kia
Chứng minh rằng các bất phương trình sau đây vô nghiệm :
a) \(x^2+\dfrac{1}{x^2+1}< 1\)
b) \(\sqrt{x^2-x+1}+\dfrac{1}{\sqrt{x^2-x+1}}< 2\)
c) \(\sqrt{x^2+1}+\sqrt{x^4-x^2+1}< 2\sqrt[4]{x^6+1}\)
Chứng minh rằng các bất phương trình vô nghiệm
a) \(\sqrt{x-3}+\sqrt{2-x}\ge3+x\)
b)\(\sqrt{3+x^{ }2}-\sqrt{5+x^{ }2}>1\)
c)2x2 + x < 5x - 2
d)2x2 + 3 ≤ 2x - 1
GIÚP HỘ VỚI. THANK YOU
Cho điểm M nằm ngoài đường tròn (O;R) . Từ điểm M kẻ hai tiếp tuyến MA,MB với đường tròn ( A,B là hai tiếp điểm)
A) chứng minh tứ giác MAOB nội tiếp
B) Qua A kẻ đường thẳng song song với MB cắt đường tròn (O;R) tại C . Nối MC cắt đường tròn (O;R) tại D. Tia AD cắt MB tại E. Chứng minh EM=EB
Cho đẳng thức : a(b-c)x2 +b(c-a)xy +c(a-b)y2 đúng với mọi x,y và cho a,b,c khác
Chứng minh :\(\dfrac{2}{b}\) =\(\dfrac{1}{a}\) +\(\dfrac{1}{c}\)
Chứng minh :
a) a\(a^4 + b^4 +c^2 ≥ 2a(ab^2 -a+c+1)+a^2(1+b^2)+b^2(1+c^2)+c^2(a+a^2) ≥6abc\)
b) \(\dfrac{1}{a+b-c}+\dfrac{1}{b+c-a}+\dfrac{1}{c+a-b}\text{≥}\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)
\(\dfrac {\sqrt {x+1} \sqrt{2x-1}} {x-1} \leq 0\)
\(\Leftrightarrow \dfrac {(x+1-2x+1)(x+1-4)} {x-1} \leq 0\)
Mình cần chi tiết cách để tính ra được bất phương trình tương đương này. Nhờ các bạn giúp mình nhé. Minh cảm ơn

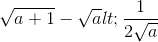 ,a>0
,a>0







