\(\sin^4x-\cos^4x=\left(\sin^2x+\cos^2x\right)\left(\sin^2x-\cos^2x\right)=\sin^2x-\cos^2x\)
Đúng 2
Bình luận (0)
\(\sin^4x-\cos^4x=\left(\sin^2x+\cos^2x\right)\left(\sin^2x-\cos^2x\right)=\sin^2x-\cos^2x\)
Chứng minh đẳng thức sau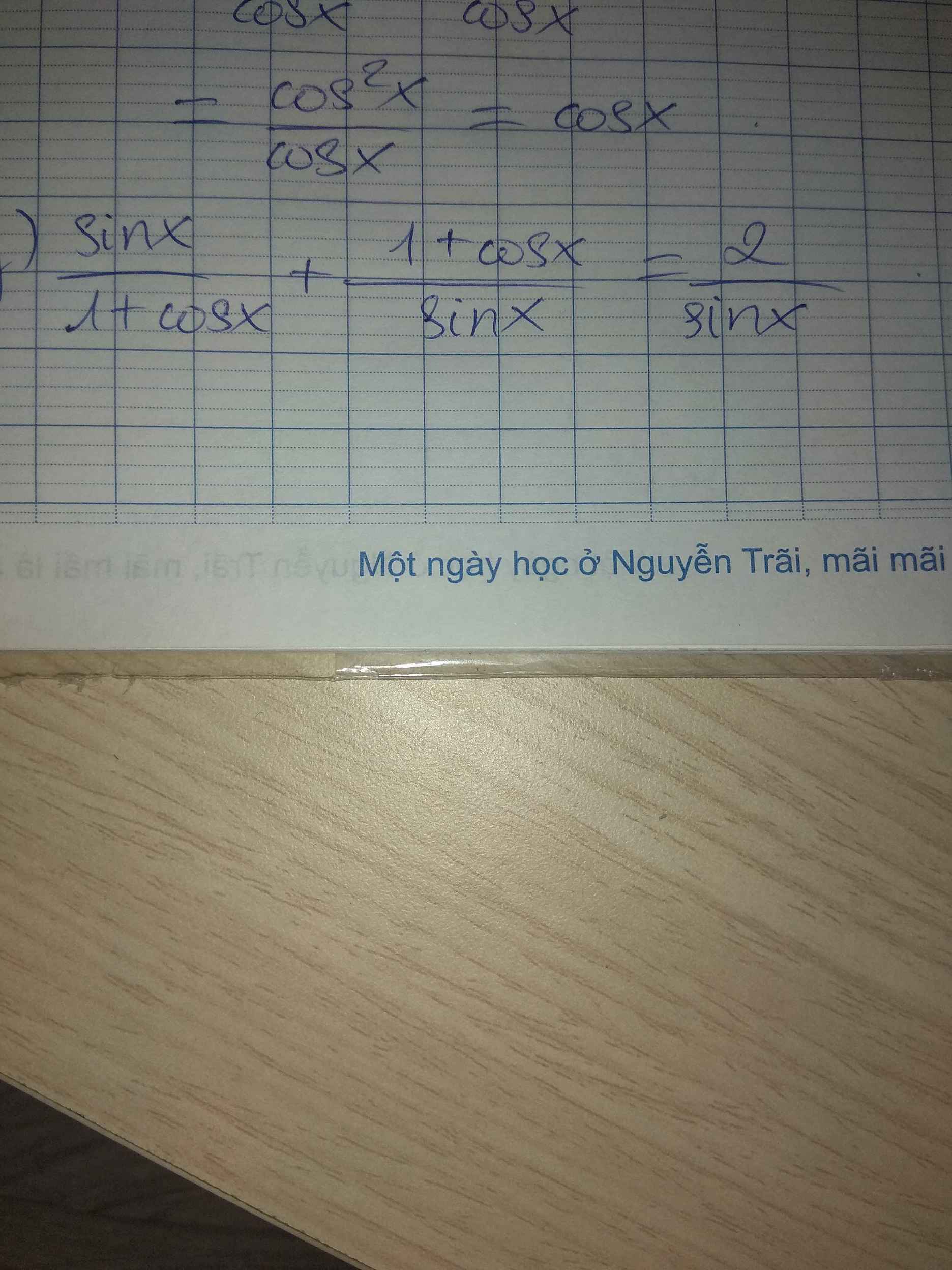
Chứng minh đẳng thức sau: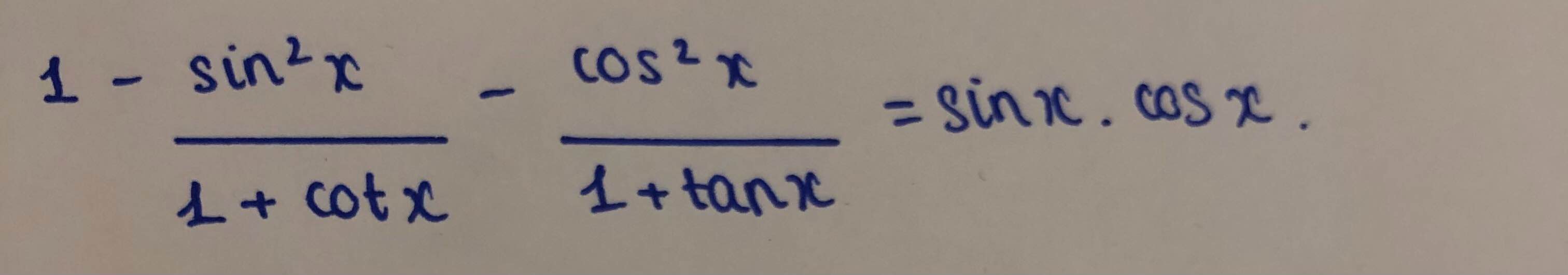
Chứng minh đẳng thức sau: Tanx/sinx - sinx/cotx = cosx
Chứng minh đẳng thức sau : Tan²x - sin²x= tan²x .sin²x
Chứng minh đẳng thức sau
Sin^2x-tan^2× = tan^6x.(cos^2x-cot^2x)
Chứng minh đẳng thức sau
\(4cos^4x - 2cos2x - \dfrac{1}{2}cos4x = \dfrac{3}{2}\)
Chứng minh đẳng thức sau
\(\dfrac{cos^3x-cos3x}{cosx} + \dfrac{sin^3x+sin3x}{sinx} = 3\)
Chứng minh đẳng thức, đề dưới bình luận