Bài 2: Tỉ số lượng giác của góc nhọn
Các câu hỏi tương tự
Không dùng máy tính hãy tính giá trị a) A = (sin 30° -cos 60° ) + ( tan 40° . tan 50°) b) B = ( cos² 20° +cos² 70° ) - (cot 42° . cot 48°) Tôi cần gấp nên mọi người giúp ạ
bài 1 : hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của góc nhỏ hơn 45 độ : cos 60 độ , sin 67 độ , cos 72 độ , tan 80 độ , cot 20 độ
bài 2: 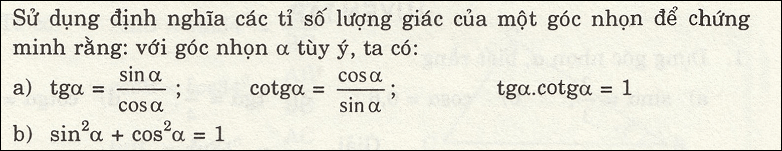
không dùng bảng số và máy tính hãy tính giá trị của các biểu thức sau :
a) A Sin210độ + Sin220 độ + ..... + Sin270 độ + Sin280 độ
b) B Cos215độ + Cos225 dộ + Cos235độ + Cos245độ + Cos255độ + Cos265độ + Cos275độ
c) C Cos212độ + Cot21độ + Cot235độ + Cot289độ + Cot237độ - 3
ai giúp e bài này với e mới học chưa hiểu lắm
Đọc tiếp
không dùng bảng số và máy tính hãy tính giá trị của các biểu thức sau :
a) A = Sin210độ + Sin220 độ + ..... + Sin270 độ + Sin280 độ
b) B = Cos215độ + Cos225 dộ + Cos235độ + Cos245độ + Cos255độ + Cos265độ + Cos275độ
c) C= Cos212độ + Cot21độ + Cot235độ + Cot289độ + Cot237độ - 3
ai giúp e bài này với e mới học chưa hiểu lắm
Không dùng máy tính:
a) So sánh tan 78 độ và cos 11 độ
b) Tính giá trị biểu thức A = tan 60 . sin^2 23 + cot 30 . sin^2 27
c) Cho sin a = 2/3 với 0< a< 90 độ. Tính cos a, tan a, cot a
a) Biết sin =9/15 .Tính cos ; tan ; cot?
b) Biết cos =3/5.Tính sin, tan, cot?
c) Biết tan =3/4. Tính cot, sin, cos?
Bài 1: a) Tính A = cos220o + cos240o + cos250o + cos270o
b) Tính B = sin225o + sin245o + sin265o + sin285o
Cho 0o x 90o, CM các biểu thức sau không phụ thuộc vào biến:
1.A2left(sin^4x+cos^4x+sin^2xcos^2xright)^2-left(sin^8x+cos^8xright)
2.Bleft(dfrac{1-tan^2x}{tan x}right)^2-left(1+tan^2xright)left(1+cot^2xright)
3.Cleft(sin^4x+cos^4x-1right)left(tan^2x+cot^2x+2right)
4.Ddfrac{tan^2x-cos^2x}{sin^2x}+dfrac{cot^2x-sin^2x}{cos^2x}
5.Edfrac{cot^2x-cos^2x}{cot^2x}+dfrac{sin xcdotcos x}{cot x}
Đọc tiếp
Cho 0o < x < 90o, CM các biểu thức sau không phụ thuộc vào biến:
\(1.A=2\left(\sin^4x+\cos^4x+\sin^2x\cos^2x\right)^2-\left(\sin^8x+\cos^8x\right)\)
\(2.B=\left(\dfrac{1-\tan^2x}{\tan x}\right)^2-\left(1+\tan^2x\right)\left(1+\cot^2x\right)\)
\(3.C=\left(\sin^4x+\cos^4x-1\right)\left(\tan^2x+\cot^2x+2\right)\)
\(4.D=\dfrac{\tan^2x-\cos^2x}{\sin^2x}+\dfrac{\cot^2x-\sin^2x}{\cos^2x}\)
\(5.E=\dfrac{\cot^2x-\cos^2x}{\cot^2x}+\dfrac{\sin x\cdot\cos x}{\cot x}\)
Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trịcủa các góc nhọn α.a) A cos4α + 2cos2α . sin2α + sin4ab) B sin4α + cos2α . sin2α + cos2αc) C 2(sin α - cos α )2 - (sin α + cos α )2 + 6sin α . cos αd) D (tan α - cot α )2 - (tan α + cot α )2e) E 4 cos2 α + (sin α - cos α)2 + (sin α+ cosα)2 + 2(sin2 α -cos2 α)f) F dfrac{1}{1+sintext{α}}+dfrac{1}{1-sintext{α}}-2 tan2α
Đọc tiếp
Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trị
của các góc nhọn α.
a) A = cos4α + 2cos2α . sin2α + sin4a
b) B = sin4α + cos2α . sin2α + cos2α
c) C = 2(sin α - cos α )2 - (sin α + cos α )2 + 6sin α . cos α
d) D = (tan α - cot α )2 - (tan α + cot α )2
e) E = 4 cos2 α + (sin α - cos α)2 + (sin α+ cosα)2 + 2(sin2 α -cos2 α)
f) F = \(\dfrac{1}{1+sin\text{α}}\)+\(\dfrac{1}{1-sin\text{α}}\)-2 tan2α
CMR
a)\(\frac{1+\cos\alpha}{\sin\alpha}=\frac{\sin\alpha}{1-\cos\alpha}\)
b)\(\frac{\tan\alpha+1}{\tan\alpha-1}=\frac{1+\cot\alpha}{1-\cot\alpha}\)
c) \(\tan^2\alpha-\sin^2\alpha=\tan^2\alpha.\sin^2\alpha\)
d)\(\frac{1-4\sin^2\alpha.\cos^2\alpha}{\left(\sin\alpha-\cos\alpha\right)^2}=\left(\sin\alpha+\cos\alpha\right)^2\)











