Chương I - Hệ thức lượng trong tam giác vuông
Các câu hỏi tương tự
6. Cho tam giác ABC vuông ở A đường cao AH, biết AB = 6cm, AC =8cm. a/ Tính AH; b/ Tính góc HAC; c/ Từ H kẻ HE AB, HF AC. Tính EF
Cho tam giác ABC có AC = 16cm, AB = 12cm, BC = 20cm. Đường cao AH.
a,Chứng minh tam giác ABC vuông.
b,Tính đường cao AH.
c,Từ H vẽ HE vuông góc với AB và HF vuông góc với AC. Tính HE, HF
d,So sánh: tanB và sinB (mình cần nhất câu này thôi 3 câu trên có hay không không quan trọng cảm ơn ae)
Cho ΔABC vuông tại A, AH là đường cao. Kẻ HE vuông AB tại E, HF vuông AC tại F.
a)AE.AB=AF.AC
b)EF3=BC.BE.CF
c)\(\frac{AB^2}{AC^2}=\frac{HB}{HC}\)
d)BC2=3AH2+BE2+CF2
e)\(\frac{AB^3}{AC^3}=\frac{BE}{CF}\)
f)HB.HC=AE.EB+AF.FC
g)C/m: AM vuông EF (M là trung điểm BC)
Cho tam giác ABC vuông tại A, đường cao AH (HϵBC)a) Biết AB 12cm, BC 20cm. Tính AC, B, AH (góc làm tròn đến độ)b) Kẻ HE vuông góc AB (EϵAB). Chứng minh: AE.ABAC2-HC2c) Kẻ HF vuông góc AC (FϵAC). Chứng minh: AFAE.tanC
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH (HϵBC)
a) Biết AB = 12cm, BC = 20cm. Tính AC, B, AH (góc làm tròn đến độ)
b) Kẻ HE vuông góc AB (EϵAB). Chứng minh: AE.AB=AC2-HC2
c) Kẻ HF vuông góc AC (FϵAC). Chứng minh: AF=AE.tanC
Tam giác ABC vuông tại A,đường cao AH ;HE vuông góc AB;HF vuông góc AC
1,CM:AE*ABAF*AC
2,CM:tam giác AEF đồng dạng tam giác ACB
3,Cho BH8cm;CH18cm.Tính EF?
4,M là trung điểm của BC.CM:AM vuông góc EF?
5,Cho BC2a cố định .Tìm vị trí của A để S tam giác AHF max
6,Đặt ABc;ACb;BCa(a;b;c0);AHh;BEx;CFy(h,x,y0)
CM:a,frac{x}{y}frac{c^3}{b^3}
b,3h^2+x^2+y^2a^2
c,acdot xcdot yh^3
P/S:Chỉ cần làm câu 5 và 6 thôi nha
Đọc tiếp
Tam giác ABC vuông tại A,đường cao AH ;HE vuông góc AB;HF vuông góc AC
1,CM:AE*AB=AF*AC
2,CM:tam giác AEF đồng dạng tam giác ACB
3,Cho BH=8cm;CH=18cm.Tính EF?
4,M là trung điểm của BC.CM:AM vuông góc EF?
5,Cho BC=2a cố định .Tìm vị trí của A để S tam giác AHF max
6,Đặt AB=c;AC=b;BC=a(a;b;c>0);AH=h;BE=x;CF=y(h,x,y>0)
CM:a,\(\frac{x}{y}=\frac{c^3}{b^3}\)
b,\(3h^2+x^2+y^2=a^2\)
c,\(a\cdot x\cdot y=h^3\)
P/S:Chỉ cần làm câu 5 và 6 thôi nha
cho tam giác ABC vuông tại A ( AB BC) có đường cao AH. Từ H kẻ HE ⊥ AB, HF ⊥ AC ( E ∈ AB, F ∈ AC). Gọi O là giao điểm của AH và È. Chứng minh:
a) AH^3 BC. HE. HF
b) HB . HC 40E . OF
c) frac{AB^2}{AC^2} frac{HB}{HC}
d) frac{AB^3}{AC^3} frac{BE}{CF}
Đọc tiếp
cho tam giác ABC vuông tại A ( AB < BC) có đường cao AH. Từ H kẻ HE ⊥ AB, HF ⊥ AC ( E ∈ AB, F ∈ AC). Gọi O là giao điểm của AH và È. Chứng minh:
a) AH\(^3\) = BC. HE. HF
b) HB . HC = 40E . OF
c) \(\frac{AB^2}{AC^2}\) = \(\frac{HB}{HC}\)
d) \(\frac{AB^3}{AC^3}\) = \(\frac{BE}{CF}\)
Bài 3: Cho ∆ ABC vuông tại A, đường cao AH biết HB=4cm ; HC= 9cm . a) Tính AB và AH. b) Từ HE vuông góc với AB, HF vuông góc với AC Tử giác AEHF là hình gì? Tính EF ?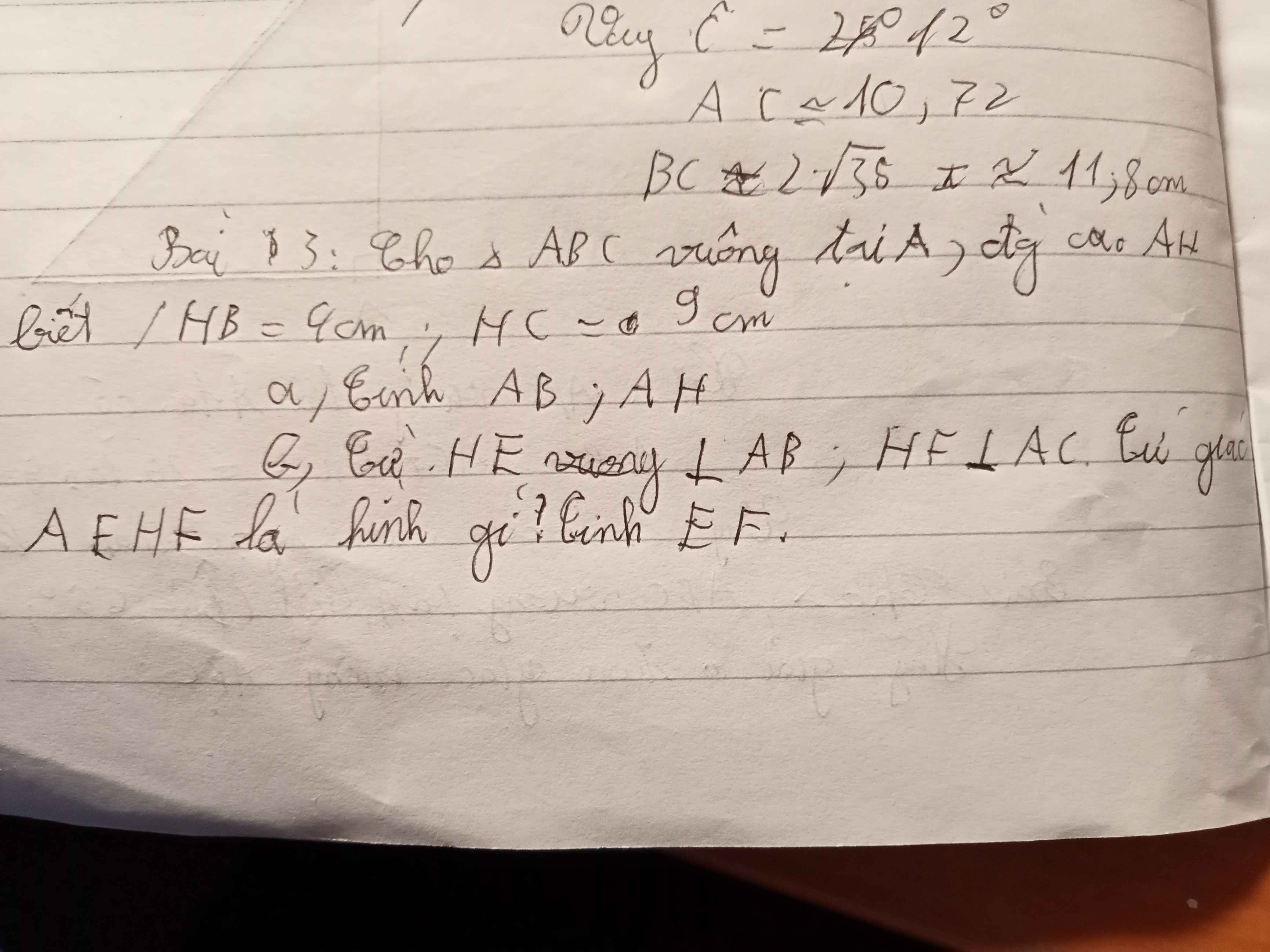
2, cho tg ABC vg tại A, dg cao AH. Từ H kẻ HE ⊥ AB, HF ⊥ AC.
a, cho BH= 9 cm; CH= 25cm. Tính AH,AB
b, CMR: AE.AB=AF.AC
c, CMR: \(\dfrac{sinB+5cosC}{sin^4B+cos^4B+2sin^2B.cos^2B}=6sinB\)
cho tam giác ABC vuông tại A đường cao AH kẻ HE vuông AB, HF vuông AC . biết AH=6cm, CH=9cm
a)tính AB, BH
b)tính HE, HF
c) ch/m AE.AB=AF.AC









