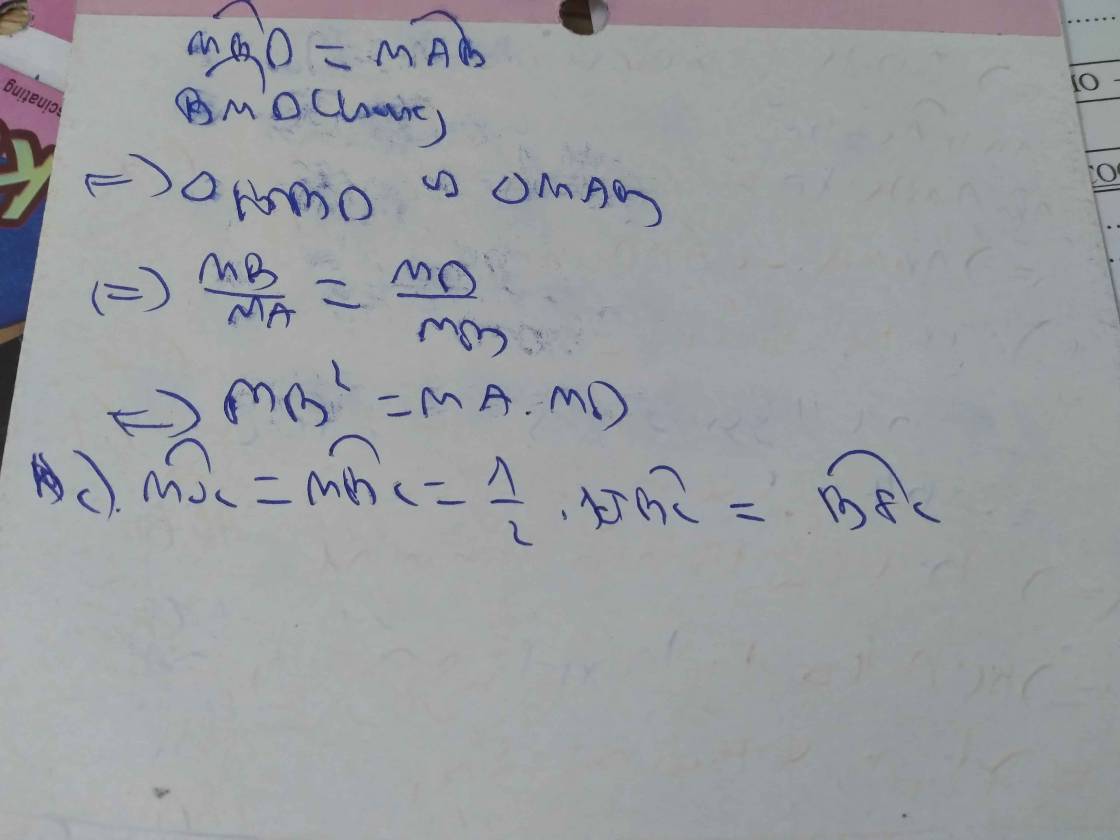Ôn thi vào 10
Các câu hỏi tương tự
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O. Các tiếp tuyến tại B và C cắt nhau tại M. Gọi D là giao điểm của AM và đường tròn tâm O. Gọi H là giao điểm của OM và BC.a) c/m MBOC nội tiếp và MB. MBMA.MDb) Tia AH cắt (O) tại E. C/m HO.HMHA.HE và tứ giác OEMA nội tiếp.c) Gọi N là giao điểm của AB và EC. C/m MN//BC.Mọi người giúp mình câu c) với ạ. mình chân thành cảm ơn.
Đọc tiếp
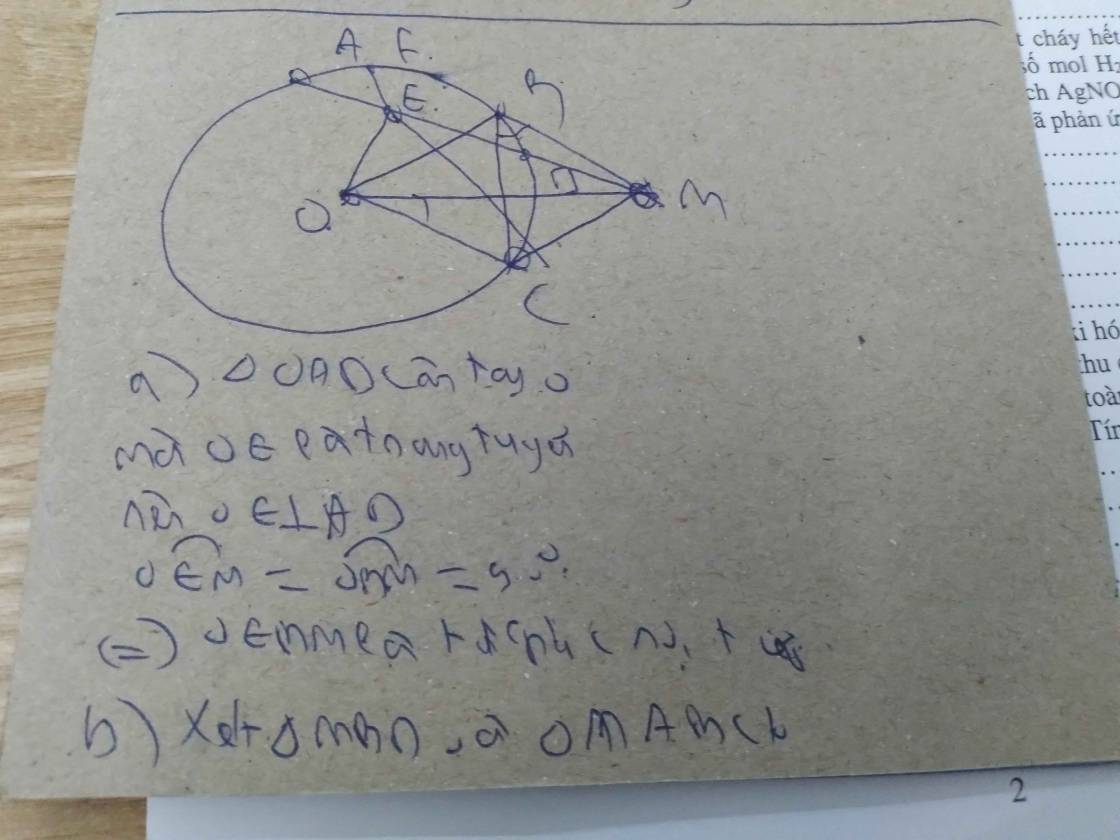
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O. Các tiếp tuyến tại B và C cắt nhau tại M. Gọi D là giao điểm của AM và đường tròn tâm O. Gọi H là giao điểm của OM và BC.
a) c/m MBOC nội tiếp và MB. MB=MA.MD
b) Tia AH cắt (O) tại E. C/m HO.HM=HA.HE và tứ giác OEMA nội tiếp.
c) Gọi N là giao điểm của AB và EC. C/m MN//BC.
Mọi người giúp mình câu c) với ạ. mình chân thành cảm ơn.
Cho tam giác nhọn ABC (ABAC) nội tiếp đường tròn (O). Các đường cao AD, BE cắt nhau tại H. Tiếp tuyến tại A của (O) cắt đường thằng BC tại M.a) C/M tứ giác DHEC nội tiếpb)CM 4 điểm A,B,D,E cùng thuộc 1 đg trònc)CM MA2MB.MCd) AD cắt (O) tại điểm thứ hai là I.Vẽ đường kính AK của (O).CM BKCIe) Kẻ IF vuông góc với AB (F thuộc AB). FD cắt AC tại .CM IN//BEGiải hộ em câu d và e thôi ạ mấy câu kia giải hay không cũng được.
Đọc tiếp
Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Các đường cao AD, BE cắt nhau tại H. Tiếp tuyến tại A của (O) cắt đường thằng BC tại M.
a) C/M tứ giác DHEC nội tiếp
b)CM 4 điểm A,B,D,E cùng thuộc 1 đg tròn
c)CM MA2=MB.MC
d) AD cắt (O) tại điểm thứ hai là I.Vẽ đường kính AK của (O).CM BK=CI
e) Kẻ IF vuông góc với AB (F thuộc AB). FD cắt AC tại .CM IN//BE
Giải hộ em câu d và e thôi ạ mấy câu kia giải hay không cũng được.
Cho tam giác ABC có 3 góc nhọn nội tiếp (O;R);(AB>AC).Gọi M là điểm chính giữa cung BC; OM cắt BC tại D; AM cắt BC tại K a)chứng minh AM là tia phân giác của BAC b)Tiếp tuyến tại A của đường tròn tâm O cắt BC tại S.Chứng minh SA²=SB.SC c)chứng minh SA=SK và S;A;O;D cùng thuộc 1 đường tròn d)Trên đường tròn tâm O đặt E sao cho SB.SC=SE² chứng minh điểm E nằm trên đường tròn (SAOD)
Cho tam giác ABC có 3 góc nhọn nội tiếp (O;R);(AB>AC).Gọi M là điểm chính giữa cung BC; OM cắt BC tại D; AM cắt BC tại K a)chứng minh AM là tia phân giác của BAC b)Tiếp tuyến tại A của đường tròn tâm O cắt BC tại S.Chứng minh SA²=SB.SC c)chứng minh SA=SK và S;A;O;D cùng thuộc 1 đường tròn d)Trên đường tròn tâm O đặt E sao cho SB.SC=SE² chứng minh điểm E nằm trên đường tròn (SAOD)
Cho tam giác ABC có 3 góc nhọn, AB AC và nội tiếp đường tròn (O). Ba đường cao AD, BE, CF cắt nhau tại H. Tia AD cắt đường tròn (O) ở K( K khác A). Tiếp tuyến tại C của đường tròn (O) cắt đường thẳng FD tại M.a) Chứng minh tứ giác ACDF nội tiếpb) AM cắt đường tròn (O) tại I( I khác A). Chứng minh MC2 MI. MA và tam giác CMD cân.c) MD cắt BI tại N. Chứng minh 3 điểm C, K, N thẳng hàng.Giúp mình với ạ
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn, AB < AC và nội tiếp đường tròn (O). Ba đường cao AD, BE, CF cắt nhau tại H. Tia AD cắt đường tròn (O) ở K( K khác A). Tiếp tuyến tại C của đường tròn (O) cắt đường thẳng FD tại M.
a) Chứng minh tứ giác ACDF nội tiếp
b) AM cắt đường tròn (O) tại I( I khác A). Chứng minh MC2 = MI. MA và tam giác CMD cân.
c) MD cắt BI tại N. Chứng minh 3 điểm C, K, N thẳng hàng.
Giúp mình với ạ
Câu 4. (3,0 điểm) Cho tam giác ABC nhọn nội tiếp (O), hai đường cao BD và CE của tam giác ABC cắt nhau tại H. Vẽ DK vuông góc với AB (K thuộc AB), gọi F là trung điểm của ED, tia BF cắt (O) tại I (khác B), a) Chứng minh tứ giác BEDC nội tiếp b) Chứng minh rằng BK.BA BF.BI c) Chứng minh rằng, hai đường thẳng AH và ID cắt nhau tại một điểm nằm trên (O).
Đọc tiếp
Câu 4. (3,0 điểm) Cho tam giác ABC nhọn nội tiếp (O), hai đường cao BD và CE của tam giác ABC cắt nhau tại H. Vẽ DK vuông góc với AB (K thuộc AB), gọi F là trung điểm của ED, tia BF cắt (O) tại I (khác B),
a) Chứng minh tứ giác BEDC nội tiếp
b) Chứng minh rằng BK.BA = BF.BI
c) Chứng minh rằng, hai đường thẳng AH và ID cắt nhau tại một điểm nằm trên (O).
từ điểm m nằm ngoài đường tròn (o) vẽ 2 tiếp tuyến ma mb gọi E là trung điểm cuả MB đường thẳng AE cắt (O) tại C,MC cắt (O) tại D ,H là giao điểm của AB và MO a) chứng minh HE// AM b) chứng minh tứ giác HCEB nội tiếp và AD // MBc) gọi F là giao điểm của BO và(O) K là giao điểm của AD và MF chứng minh KD =3KA
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Vẽ 3 đường cao AD, BE, CF cắt nhau tại trực tâm H. Các tiếp tuyến tại B, C của (O) cắt nhau tại S. AS cắt EF, DE, (O), BC tại I, L, K, J. Gọi M là trung điểm BC, N là trung điểm AB.a) CMR BFEC nội tiếp và AE.ACAF.ABb) CMR SA/SKJA/JKc) CMR I là trung điểm EFd) CMR L, M, N thẳng hàngEm xin cảm ơn!
Đọc tiếp
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Vẽ 3 đường cao AD, BE, CF cắt nhau tại trực tâm H. Các tiếp tuyến tại B, C của (O) cắt nhau tại S. AS cắt EF, DE, (O), BC tại I, L, K, J. Gọi M là trung điểm BC, N là trung điểm AB.
a) CMR BFEC nội tiếp và AE.AC=AF.AB
b) CMR SA/SK=JA/JK
c) CMR I là trung điểm EF
d) CMR L, M, N thẳng hàng
Em xin cảm ơn!
cho tam giác ABC nội tiếp đường tròn tâm (o), đường kính AB2R trên cạnh BC lấy điểm M ( M khác B và C) đường thẳng AM cắt đường tròn O tại D, đường thẳng BD cắt AC tại E đường tròn tâm I ngoại tiếp tam giác MDB cắt đường kính ad tại điểm thứ hai là N1) chứng minh tứ giác CEDM nội tiếp đường tròn và 3 điểm E,M,N thẳng hàng2)cho đoạn thẳng CN cắt đường tròn(i) ở F .cmr : DF//AE
Đọc tiếp
cho tam giác ABC nội tiếp đường tròn tâm (o), đường kính AB=2R trên cạnh BC lấy điểm M ( M khác B và C) đường thẳng AM cắt đường tròn O tại D, đường thẳng BD cắt AC tại E đường tròn tâm I ngoại tiếp tam giác MDB cắt đường kính ad tại điểm thứ hai là N
1) chứng minh tứ giác CEDM nội tiếp đường tròn và 3 điểm E,M,N thẳng hàng
2)cho đoạn thẳng CN cắt đường tròn(i) ở F .cmr : DF//AE