Cho tam giác đều ABC, đường cao AD, H là trực tâm của tam giác. M là điểm bất kỳ thuộc BC, gọi E và F theo thứ tự là hình chiếu của M lên AB, AC. Gọi I là trung điểm của AM.
a) tứ giác DEIF là hình gì ?vì sao
b) chứng minh MH, ID, EF đồng quy
c) xác định vị trí của M trên BC để EF có độ dài nhỏ nhất
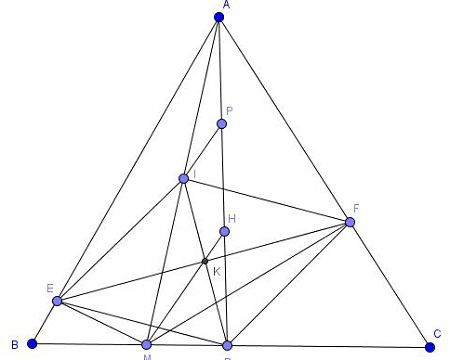
a) Các tam giác vuông AEM và ADM có EI và DI là trung tuyến ứng với AM nên
=> EI = DI ( = ½ AM)
=> Tam giác EID cân tại I
Lại có các tam giác AEI và ADI cân tại I nên:
^EIM = 2^EAI và ^MID = 2^IAD
=> ^EID = ^EIM + ^MID = 2(^EAI + ^IAD) = 2^EAD = 2. 30 = 60 độ
(Vì AD là đường cao nên là phan giác ^A)
Tam giác EID cân lại có ^EID = 60 độ nên đều
Tương tự tam giác IFD đều nên: EI = IF = FD = DE => Tứ giác DEIF là hình thoi
b) Gọi O là giao EF và DI và K là trung điểm AH, ta có IK là trng bình tam giác AMH và OH là trung bình tam giác AID.
=> HO//IK và HM//IK
=> Tia HO và HM trùng nhau hay M, H, O thẳng hàng => MH, ID, EF đồng quy tại O







