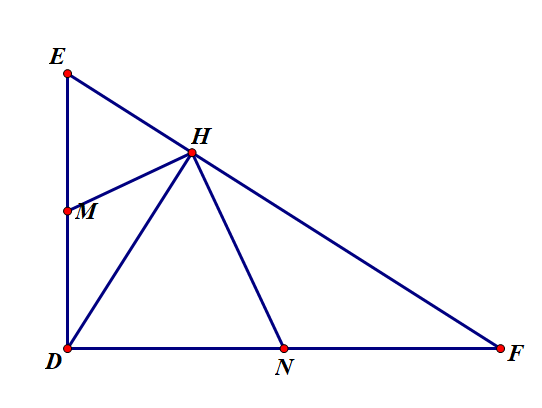
\(\text{Xét tam giác EHD vuông tại H có đường trung tuyến HM ứng với cạnh huyền ED}\)
\(\Rightarrow MH=MD=ME=\dfrac{1}{2}ED\)
\(\Rightarrow\)Tam giác HMD cân tại M
\(\Rightarrow\)\(\widehat{MHD}=\widehat{MDH}\)
Tương tự với tam giác DHF vuông tại H ta được \(\widehat{DHN}=\widehat{HDN}\)
Ta có \(\widehat{MHN}=\widehat{MHD}+\widehat{NHD}=\widehat{MDH}+\widehat{NDH}=\widehat{MDN}\)
Suy ra góc MHN có số đo 90 độ
Tick nha bạn 😘
Ta có: ΔDHE vuông tại H(Gt)
mà HM là đường trung tuyến ứng với cạnh huyền DE(Gt)
nên HM=DM=ME
Ta có: ΔDHF vuông tại H(gt)
mà HN là đường trung tuyến ứng với cạnh huyền DF(Gt)
nên HN=DN=FN
Xét ΔNDM và ΔNHM có
ND=NH(cmt)
NM chung
MD=MH(cmt)
Do đó: ΔNDM=ΔNHM(c-c-c)
Suy ra: \(\widehat{NDM}=\widehat{NHM}\)
hay \(\widehat{NHM}=90^0\)














