`a,` Xét Tam giác `BAE` và Tam giác `BIE` có:
`BA = BI (g``t)`
\(\widehat{ABE} =\widehat{IAE}\) (tia phân giác \(\widehat{ABI}\))
`AE` chung
`=>` Tam giác `BAE =` Tam giác `BIE (c-g-c)`
`b,` vì Tam giác `BAE =` Tam giác `BIE` (a)
`=>` \(\widehat{BAE}=\widehat{BIE}=90^0\) (2 góc tương ứng)
`=> \(EI\perp BC\)
`c,` Xét Tam giác `BAH và` Tam giác `BIH`
`BA=BI (g``t)`
\(\widehat{BAH}=\widehat{BIH}\) (tia phân giác \(\widehat{ABI}\))
`AH` chung
`=>` Tam giác `BAH =` Tam giác `BIH (c-g-c)`
`=>` \(\widehat{BHA}=\widehat{BHI}\) (2 góc tương ứng)
mà 2 góc này ở vị trí kề bù
`=>`\(\widehat{BHA}+\widehat{BHI}=180^0\)
`=>` \(\widehat{BHA}=\widehat{BHI} =\) \(\dfrac{180}{2}=90^0\)
`=>` \(BE\perp AI\) (đpcm)
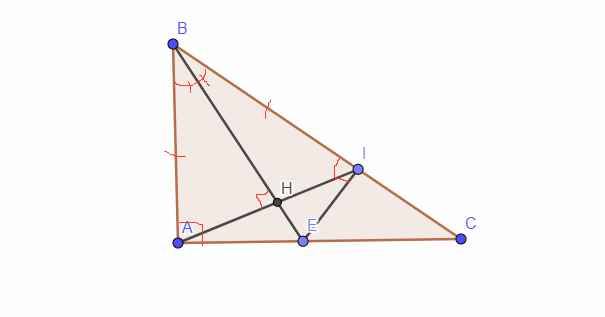
*Hình đây nha cậu, xl nãy làm bài mình quên gửi:').












