Bài 3: Tính chất đường phân giác của tam giác
Các câu hỏi tương tự
Cho tam giác ABC vuông tại A (AB < AC), kẻ đường cao AH, đường trung tuyến AM. Đường thẳng vuông góc với AM tại A cắt đường thẳng BC tại D. Chứng minh rằng: a) AB là tia phân giác của góc DAH. b) BH.CD = BD.CH
Cho tam giác ABC vuông tại A (AB < AC), kẻ đường cao AH, đường trung tuyến AM. Đường thẳng vuông góc với AM tại A cắt đường thẳng BC tại D. Chứng minh rằng:
a) AB là tia phân giác của góc DAH.
b) BH.CD = BD.CH
Cho tam giác ABC vuông tại A(AB<AC), kẻ đường cao AH, trung tuyến AM. Đường thẳng vuông góc với AM tại A cắt đường thằng BC tại D. Chứng minh:
a)AB là tia phần giác của DAH
b)BH.CD=BD.CH
Cho tam giác abc có AB=16cm Ac=32cm BC=21cm. Đường phân giác trong vài ngoài của góc A cắt BC lần lượt tại D và E. a) Cm B là trung điểm của EC b) Tính DE
Cho ABC vuông tại A , đường cao AH Chứng minh : ABH - CBA . Từ đó tính BH khi AB = 6 cm , AC = 8 cm . b ) Gọi P , Q lần lượt là trung điểm của CH , AH . Đường thẳng BQ cắt đường thẳng AP tại N , đường thẳng PQ cắt đường thẳng AB tại M. Chứng minh : Q là trực tâm tam giác ABP c ) Chứng minh : NB là tia phân giác của góc MNH
Bài 3 (3 điểm): Cho ∆ABC có:Kẻ đường cao AH (H ∈ BC ), tia phân giác góc A cắt BC tại D.a) Chứng minh ∆HBA đồng dạng với ∆ABC và AB2 BH.BCb) Tính độ dài BC, BD và CD.c) Tính tỉ số diện tích tam giác ABD và tam giác ACD.d) Từ D kẻ DE vuông góc với AC (E ∈ AC). Tính độ dài đoạn DE.
Đọc tiếp
Bài 3 (3 điểm): Cho ∆ABC có:
![]()
Kẻ đường cao AH (H ∈ BC ), tia phân giác góc A cắt BC tại D.
a) Chứng minh ∆HBA đồng dạng với ∆ABC và AB2 = BH.BC
b) Tính độ dài BC, BD và CD.
c) Tính tỉ số diện tích tam giác ABD và tam giác ACD.
d) Từ D kẻ DE vuông góc với AC (E ∈ AC). Tính độ dài đoạn DE.
Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Gọi BD là đường phân giác của tam giác ABC.
a) Tính độ dài DA, DC.
b) Tia phân giác của góc C cắt BD tại I. Gọi M là trung điểm của BC. Chứng minh \(\widehat{BIM}\) = 90o
Cho tam giác ABC có AB=12cm, AC=20cm, BC=28cm. Đường phân giác góc A cắt BC tại D. Qua D kẻ DE//AB (E∈AC). a)Tính BD,DC,DE. b)Tính tỉ số diện tích ΔABD và ΔACD. c)Biết diện tích ΔABC=S, tính diện tích các tam giác ABD,ADE và DCE.
Xem chi tiết
Tam giác ABC có AB = 15cm, AC = 20 cm, BC = 25 cm. Đường phân giác góc BAC cắt cạnh ABC tại D (h.14)
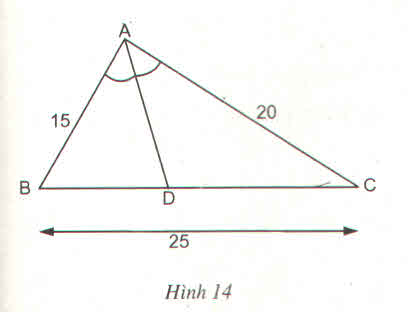
a) Tính độ dài các đoạn thẳng DB và DC
b) Tính tỉ số diện tích của hai tam giác ABD và ACD









