Ôn tập chương IV
Các câu hỏi tương tự
6. Bất đẳng thức
Bài 9: Cho a, b, c, d, e in R. Chứng minh các bất đẳng thức sau:
a. a^2+b^2+c^2ge ab+bc+ca
b. a^2+b^2+1ge ab+a+b
c. a^2+b^2+c^2+3ge2left(a+b+cright)
d. a^2+b^2+c^2ge2left(ab+bc-caright)
e. a^4+b^4+c^2+1ge2aleft(ab^2-a+c+1right)
f. frac{a^2}{4}+b^2+c^2ge ab-ac+2bc
g. a^2left(1+b^2right)+b^2left(1+c^2right)+c^2left(1+a^2right)ge6abc
h. a^2+b^2+c^2+d^2+e^2ge aleft(b+c+d+eright)
i. frac{1}{a}+frac{1}{b}+frac{1}{c}gefrac{1}{sqrt{ab}}+frac{1}{sqrt{bc}}+frac{1}{sqrt{ca}} với...
Đọc tiếp
6. Bất đẳng thức
Bài 9: Cho a, b, c, d, e \(\in\) R. Chứng minh các bất đẳng thức sau:
a. \(a^2+b^2+c^2\ge ab+bc+ca\)
b. \(a^2+b^2+1\ge ab+a+b\)
c. \(a^2+b^2+c^2+3\ge2\left(a+b+c\right)\)
d. \(a^2+b^2+c^2\ge2\left(ab+bc-ca\right)\)
e. \(a^4+b^4+c^2+1\ge2a\left(ab^2-a+c+1\right)\)
f. \(\frac{a^2}{4}+b^2+c^2\ge ab-ac+2bc\)
g. \(a^2\left(1+b^2\right)+b^2\left(1+c^2\right)+c^2\left(1+a^2\right)\ge6abc\)
h. \(a^2+b^2+c^2+d^2+e^2\ge a\left(b+c+d+e\right)\)
i. \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{1}{\sqrt{ab}}+\frac{1}{\sqrt{bc}}+\frac{1}{\sqrt{ca}}\) với a, b, c >0
k. \(a+b+c\ge\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\) với a, b, c \(\ge\)0
Cho a, b, c là 3 số thực thỏa mãn điều kiện \(a^3>36\) và \(abc=1\)
Xét tam thức bậc hai : \(f\left(x\right)=x^2-ax-3bc+\dfrac{a^2}{3}\)
a) Chứng minh rằng \(f\left(x\right)>0;\forall x\)
b) Từ câu a) suy ra \(\dfrac{a^2}{3}+b^2+c^2>ab+bc+ca\)
cho a,b và c là các số thực không âm thỏa mãn a+b+c=1
Chứng minh \(\dfrac{ab}{c+1}+\dfrac{bc}{a+1}+\dfrac{ca}{b+1}\le\dfrac{1}{4}\)
Đường tròn nội tiếp tam giác ABC tiếp xúc với các cạnh BC, CA,AB lần lượt tại E, H, M \(\Rightarrow S_{EHM}\)=?
Giải bất đẳng thức sau:
(Kx2+ 2x -2)/ (k-1)(x2-kx-3)>0 biết
kz = 2 và ky =-2 và z2 + ky2 - yk2 = 0 ( Đk: z + y = k)
Mong mọi giúp em ạ. Em chân thành cảm ơn ạ .
Giải cho tiết giúp em mấy câu này với ạ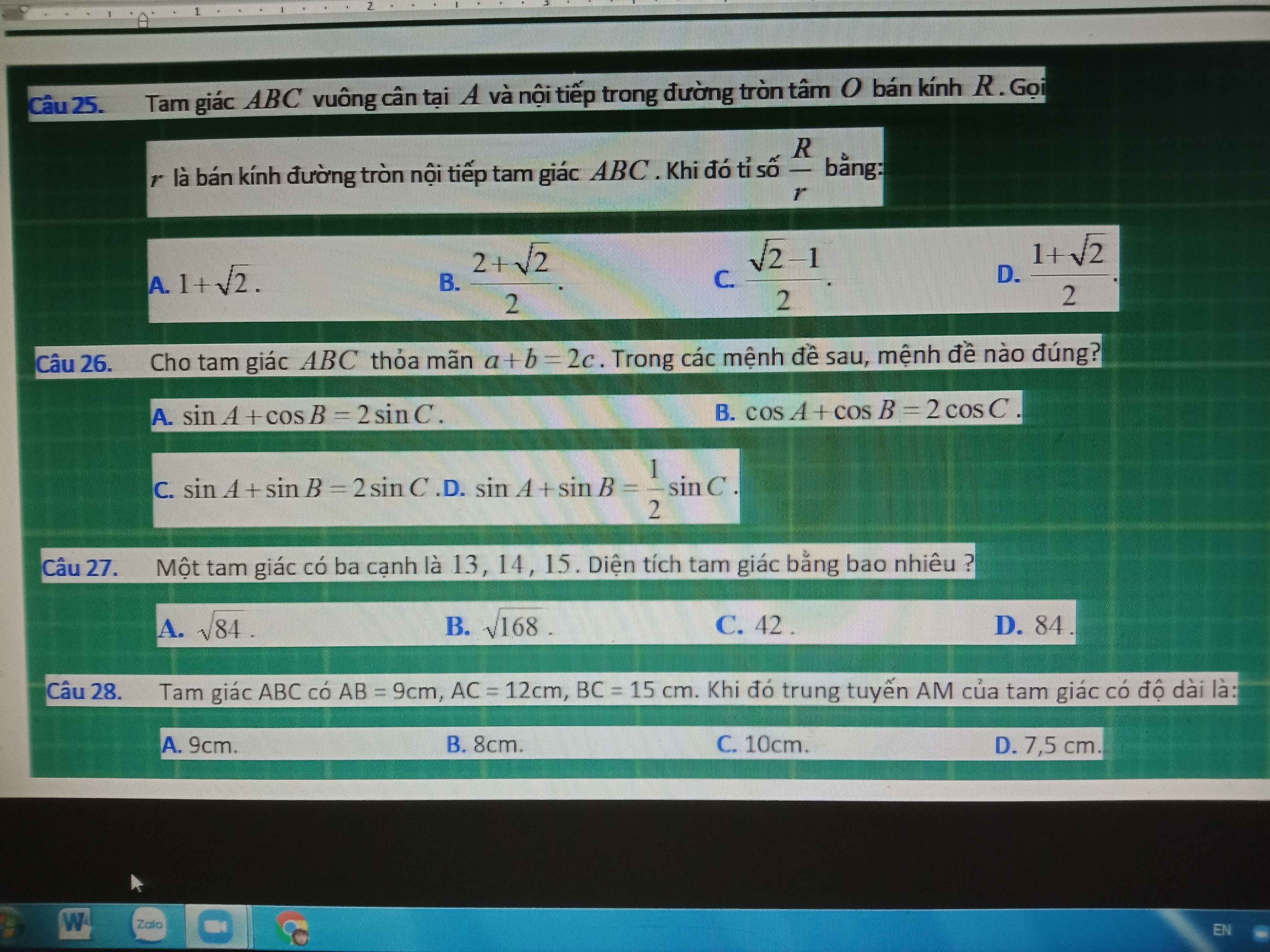
Câu 1: Tìm m để biểu thức sau luôn âm: (m-4)x2+ (m+1)x + 2m-1
Câu 2: Tìm m để bất phương trình sau có nghiệm đúng với mọi x:
a/ \(\dfrac{3x^2-5x+4}{\left(m-4\right)x^2+\left(1+m\right)x+2m-1}>0\)
b/ \(-4< \dfrac{2x^2+mx-4}{-x^2+x-1}< 6\)
GIÚP MÌNH VỚI Ạ!!!
a, <a/b+b/a>*<a/b+b/a2>≥4/căn ab
b, <a+1/b>*<b+1/c>*<c+1/a> ≥8
c, ab/c+bc/a+ca/b ≥ a+b+c
d, a/b2+b/c2+c/a2 ≥ 1/a +1/b+1/c

giúp mk giải chi tiết 5,6,7,8 vs ạ
thanks










