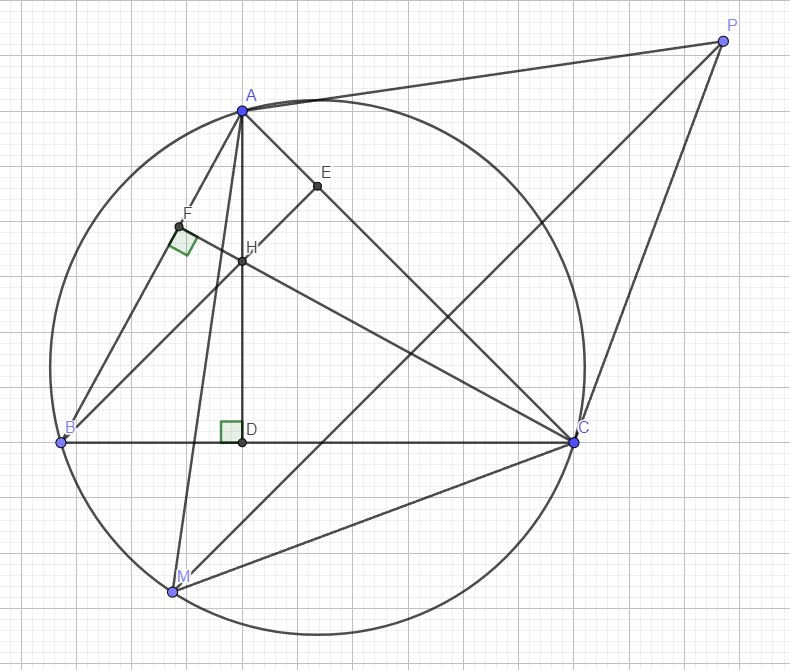
Cho tam giác ABC nội tiếp đường tròn (O) với trực tâm H .Giả sử M là 1 điểm trên cung BC không chứ A( M khác B, C).Gọi N,P theo thứ tự là điểm đối xứng của M qua các đường thẳng AB,AC.Chứng minh rằng tứ giác AHCP và tứ giác AHBN nội tiếp
CÁC BẠN ƠI GIÚP MÌNH VỚI Ạ ! MÌNH ĐANG CẦN GẤP ! MÌNH CẢM ƠN NHIỀU Ạ !
Phương pháp chứng minh 2 tứ giác nội tiếp là giống hệt nhau, nên chỉ cần c/m 1 cái còn cái kia làm tương tự.
Gọi 3 đường cao là AD, BE, CF
D và F cùng nhìn BH dưới 1 góc vuông nên BDHF nội tiếp
\(\Rightarrow\widehat{ABC}+\widehat{DHF}=180^0\)
Mà \(\widehat{DHF}=\widehat{AHC}\) (đối đỉnh)
\(\Rightarrow\widehat{ABC}+\widehat{AHC}=180^0\) (1)
\(\widehat{ABC}=\widehat{AMC}\) (cùng chắn AC) (2)
\(\widehat{AMC}=\widehat{APC}\) (do M đối xứng P qua AC) (3)
(1);(2);(3) \(\Rightarrow\widehat{AHC}+\widehat{APC}=180^0\)
\(\Rightarrow AHCP\) nội tiếp