Bài 1: Định lý Talet trong tam giác
Các câu hỏi tương tự
cho tam giác ABC.gọi I là điểm nằm trong tam giác ABC.IA,IB,IC lần lượt cắt BC,CA,AB tại M,N,P.qua A kẽ,d song song với BC,d cắt BN tại E,cắt CB tại F CMR:NA/NC+PA/PB=IA/IM
Cho tam giác ABC, kẻ Cx// AB, E là trung điểm của AB. Qua E vẽ đường thẳng song song với BC cắt AC tại D, cắt Cx tại F. BF \(\cap AB=I\)
a, Cm: IC2= IA . ID
b, Tính \(\dfrac{ID}{IC}=?\)
Cho tam giác ABC, đường thẳng song song BC cắt AB, AC tại D và E. Vẽ đường thẳng a đi qua A và song song với BC. Đường thẳng a cắt BE và CD lần lượt tại G và K. Chứng minh A là trung điểm KG
Cho hình thang ABCD có AB //CD và AB CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
Chứng minh rằng :
a) dfrac{MA}{AD}dfrac{NB}{BC}
b) dfrac{MA}{MD}dfrac{NB}{NC}
c) dfrac{MD}{DA}dfrac{NC}{CB}
Hướng dẫn : Kéo dài các tia DA, CB cắt nhau tại E (h.3), áp dụng định lí Ta - let trong tam giác và tính chất của tỉ lệ thức để chứng minh
Đọc tiếp
Cho hình thang ABCD có AB //CD và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
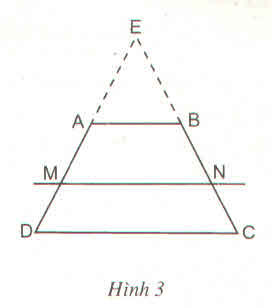
Chứng minh rằng :
a) \(\dfrac{MA}{AD}=\dfrac{NB}{BC}\)
b) \(\dfrac{MA}{MD}=\dfrac{NB}{NC}\)
c) \(\dfrac{MD}{DA}=\dfrac{NC}{CB}\)
Hướng dẫn : Kéo dài các tia DA, CB cắt nhau tại E (h.3), áp dụng định lí Ta - let trong tam giác và tính chất của tỉ lệ thức để chứng minh
1, Cho hình thang ANCD (AB // CD), M là trung điểm của CD. Gọi I là giao điểm của AM và BD, K là giao điểm của BM và AC.
a, Chứng minh IK // AB.
b, Đường thẳng IK cắt AD, BC lần lượt ở E và F. CHứng minh EI IK KF.
2, Cho hình thang ABCD có đáy nhỏ CD. Từ D, vẽ đường thẳng song song với cạnh BC, cắt AC tại M và AB tại K. Từ C, vẽ đường thẳng song song với cạnh bên AD, cắt cạnh đáy AB tại F. Qua F, vẽ đường thẳng song song với đường chéo AC, cắt cạnh bên BC tại P. Chứng minh rằng:
a, MP song...
Đọc tiếp
1, Cho hình thang ANCD (AB // CD), M là trung điểm của CD. Gọi I là giao điểm của AM và BD, K là giao điểm của BM và AC.
a, Chứng minh IK // AB.
b, Đường thẳng IK cắt AD, BC lần lượt ở E và F. CHứng minh EI = IK = KF.
2, Cho hình thang ABCD có đáy nhỏ CD. Từ D, vẽ đường thẳng song song với cạnh BC, cắt AC tại M và AB tại K. Từ C, vẽ đường thẳng song song với cạnh bên AD, cắt cạnh đáy AB tại F. Qua F, vẽ đường thẳng song song với đường chéo AC, cắt cạnh bên BC tại P. Chứng minh rằng:
a, MP song song với AB.
b, Ba đường thẳng MP, CF, DB đồng qui.
VẼ HÌNH LUÔN Ạ
Cho hình thang ABCD, AB // BC. I là giao của hai đường chéo. Qua I vẽ đường thẳng song song với hai đáy cắt AD tại E , BC tại F.
a, Chứng minh IE = IF
b, Chung minh \(\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{1}{IE}\)
c, Chứng minh \(\dfrac{2}{EF}=\dfrac{1}{AB}+\dfrac{1}{CD}\)
Bài 4:Cho tam giác ABC có AB = 6cm, AC = 8cm , BC = 10cm. Lấy điểm D trên AB sao cho AD = 2cm. Qua D vẽ đường thẳng song song với BC cắt AC tại E. 1) Tính AE. 2) Qua E vẽ đường thẳng song song với AB và cắt BC tại F. Tính BF, DE. 3) Tính và so sánh các tỉ số : AD/AB , AE/AC , DE/BC
Cho tam giác ABC, đường thẳng song song với BC cắt cạnh AB, AC lần lượt tại D, E. Vẽ đường thẳng a qua A và song song với BC. Đường thẳng a cắt đường thẳng BE và CD lần lượt tại G và K
CM: A là trung điểm của của KL
Cho tam giác ABC . Điểm O nằm trong tam giác , AO giao BC tại E ; BO giao AC tại F; CO giao AB tại K. Đường thẳng d qua A và song song với BC cắt các đường BO, CO lần lượt tại M, N . Chứng minh rằng: a) AK/KB= AN/BC
b) BE/AM=EO/OA
c) CF/FA=BC/AM
d) BE/EC=AM/AN
e) AK/KBxBE/ECxCF/FA=1










