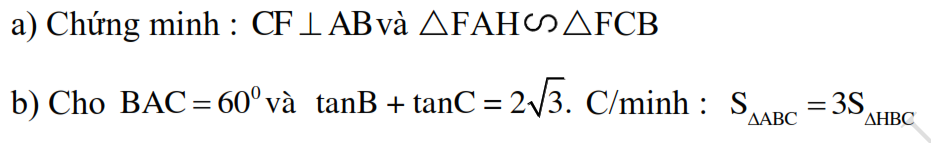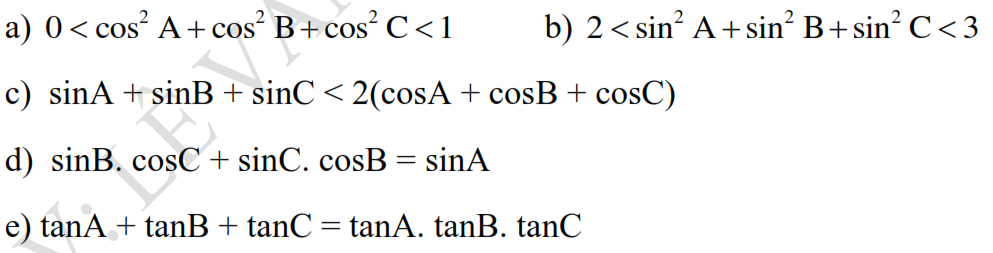a: Xét ΔBAC có
AD là đường cao ứng với cạnh BC
BE là đường cao ứng với cạnh AC
AD cắt BE tại H
Do đó: H là trực tâm của ΔBAC
Suy ra: CH\(\perp\)AB tại F
Xét ΔFAH vuông tại F và ΔFCB vuông tại F có
\(\widehat{FAH}=\widehat{FCB}\left(=90^0-\widehat{FBC}\right)\)
Do đó: ΔFAH\(\sim\)ΔFCB