Chương I - Hệ thức lượng trong tam giác vuông
Các câu hỏi tương tự
26 tháng 8 2021 lúc 16:49
Cho tam giác ABC có ba góc nhọn. Vẽ đường cao AD, BE, CF cắt nhau tại H
12 tháng 7 2021 lúc 7:36
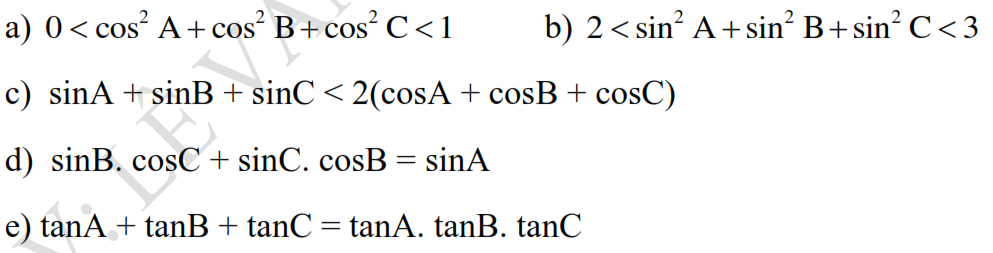
* Cho tam giác nhọn ABC có hai đường cao BD và CE cắt nhau tại H. Trên HB và HC lần lượt lấy điểm M,N sao cho góc AMC= góc ANB= \(90^0\). Chứng minh:AM=AN
* Cho tam giác ABC vuông tại A, đường cao AH. Biết \(\dfrac{AB}{AC}=\dfrac{20}{21}\)và AH=420. Tính chu vi tam giác ABC
Cho tam giác nhọn abc các đường cao AD, BE, CF cắt nhau tại H, gọi O là trung điểm của BC, I là trung điểm của AH, K là giao điểm của EF, OI .
Chứng minh AH^2= 4.IK.IO
Cho tam giác ABC có AB = 9cm,BC = 15cm,AC = 12cm.
a.Chứng minh tam giác ABC vuông tại A
b.Tính góc C,góc B.
c.Vẽ đường cao AH.Tính HA,HB,HC
cho tam giác ABC nhọn , đường cao AD,BE,EF cắt nhau tại H . CM:\(\dfrac{FE}{BC}=cosBAC\)
Bài 1 cho tam giác ABC vuông tại A , AH vuông BC, AC /AB=căn 2, HC-HB=2. Tính HC,HB,AB,AC,BC
Bài 2 cho tam giác ABC nhọn, đường cao BD cắt CE tại H, M thuộc HB, N thuộc HC sao cho AB=6 cm, AC=8 cm, BD=1 cm. Tính AH và chu vi tam giác ADE
Cho tam giác ABC nhọn. Đường cao AD, BE, CF cắt nhau tại H. Gọi M là trung điểm HC, N là trung điểm AC, AM giao với HN tại G. đường thẳng qua M vuông góc với HC cắt đường thẳng qua N vuông góc với AC tại K.
CMR:a, tam giác AEF đồng dạng tam giác ABC
b, BH.KM=BA.KN
c, \(\sqrt{\dfrac{GA^5+GB^5+GH^5}{GM^5+GK^5+GN^5}}=4\sqrt{2}\)
Cho tam giác ABC vuông tại A có đường cao AH, biết AB15, AC 20cm.a) Tính BC, AH.b) Trên đonạ HC lấy D sao cho HDHB. Tính tan góc ADH và chứng minh: HD.HCHA^2c) Trên tia AH lấy điểm E sao cho H là trung điểm của AE. Đường thẳng ED cắt AC tại F. Gọi O là trung điểm của CD. Chứng minh HF vuông góc FO.d) Đoạn HF cắt AD tại S. Tia CS cắt AH tại K và cắt AB tại M. Chứng minh: AB/AM +AD/AS AE/AK
Đọc tiếp
Cho tam giác ABC vuông tại A có đường cao AH, biết AB=15, AC= 20cm.
a) Tính BC, AH.
b) Trên đonạ HC lấy D sao cho HD=HB. Tính tan góc ADH và chứng minh: HD.HC=HA^2
c) Trên tia AH lấy điểm E sao cho H là trung điểm của AE. Đường thẳng ED cắt AC tại F. Gọi O là trung điểm của CD. Chứng minh HF vuông góc FO.
d) Đoạn HF cắt AD tại S. Tia CS cắt AH tại K và cắt AB tại M. Chứng minh: AB/AM +AD/AS = AE/AK
Cho \(\Delta ABC\) có 3 góc nhọn; đường cao AH, BE, CF cắt nhau ở H.
a) C/m \(BH.BE+HC.EC=BC^2\)
b) C/m \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=1\)
c) C/m H là giao điểm của các đường phân giác của \(\Delta DEF\)