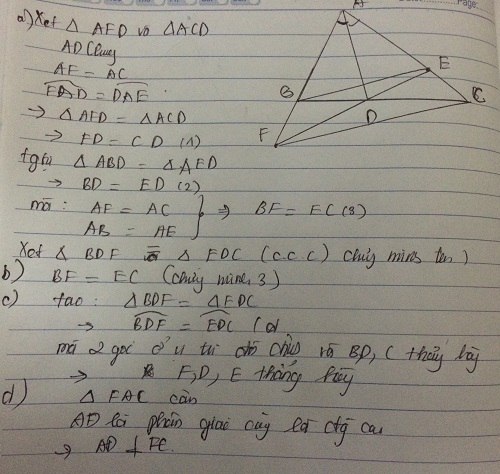Question

cho tam giác ABC (AB<AC) vẽ phân giác AD của tam giác ABC (D thuộc BC) trên cạnh AC lấy điểm E sao cho AE=AB

a,chứng minh tam giác ADB=ADE

b,chứng minhAD là đường trung trực cuả BE

c,gọi F là giao điểm của AB và DE chứng minh DBF=DEC và tam giác BFD=ECD

Answer 1

Answer 2

gửi nhầm , sr bạn -.-

Answer 3

a, Xét tam giác ABD và tam giác ADE có :

AB = AE (gt)

A1=A2 ( pg AD )

AD la canh chung

\(\Rightarrow\) Tam giác ABD = tam giác ADE ( c . g .c )

b, Theo câu a, tam giác ADB= tam giác ADE

\(\Rightarrow\) AB=AE ; BD = DE

\(\Rightarrow\) A và D cùng thuộc trung trực của BE

nên đường thẳng AD là trung trực của BE

Answer 4

c, Ta co : goc ADF = goc ADB + goc BDF

goc ADC= goc ADE + goc EDC

mã gốc ADB = gốc ADE ( tam giác ABD = tam giác ADE )

goc BDF =goc EDC (doi dinh )

\(\rightarrow\) goc ADF = goc ADC

Xét tam giác ADF va ADC có :

AD là cạnh chung

goc ADF = goc ADC (cmt)

goc BAD = goc CAD

\(\rightarrow\) Tam giác ADF = ADC ( Cạnh huyền góc nhọn)

\(\rightarrow\) góc BFD = góc ACD

\(\rightarrow\) goc FBD = góc DEC

\(\Rightarrow\) Tam giac BDF = tam giac EDC

Answer 5

Bài đây Xuân !