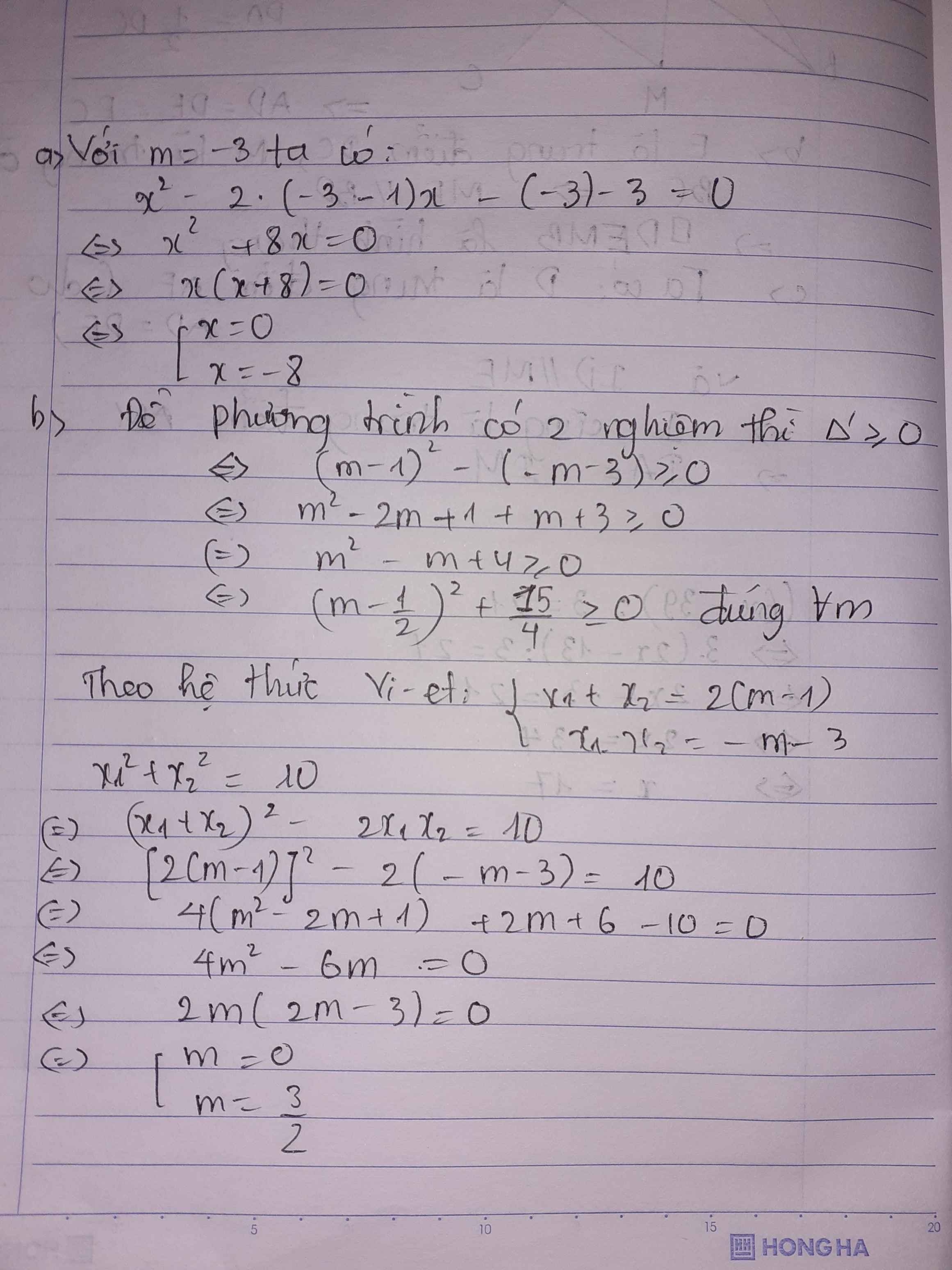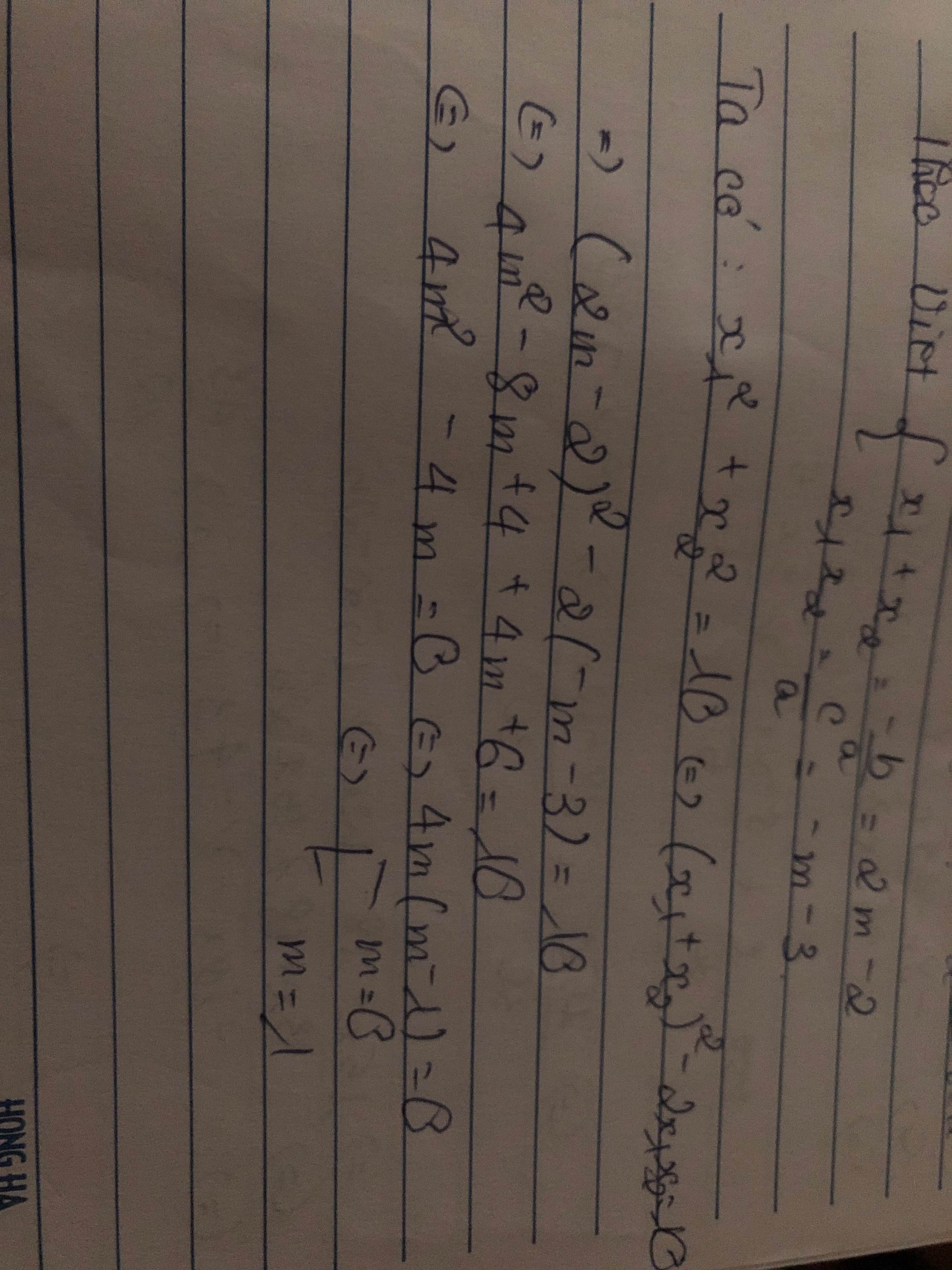a) Với m = -3 phương trình trở thành
\(x^2+8x=0\\ \Leftrightarrow x\left(x+8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\)
Vậy phương trình có tập nghiệm \(S=\left\{0;-8\right\}\)
b. Xét phương trình \(x^2-2\left(m-1\right)x-m-3=0\)
\(\Delta'=\left(m-1\right)^2-\left(-m-3\right)=m^2-2m+1+m+3=m^2-m+4=\left(m-\dfrac{1}{2}\right)^2+\dfrac{15}{4}>0\)
Suy ra, phương trình có 2 nghiệm \(x_1,x_2\) thỏa mãn \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-m-3\end{matrix}\right.\) (hệ thức Viet)
Ta có :
\(x_1^2+x_2^2=10\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\\ \Leftrightarrow4\left(m-1\right)^2+2\left(m+3\right)=10\\ \Leftrightarrow4m^2-6m=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{3}{2}\end{matrix}\right.\)
Vậy \(m\in\left\{0;\dfrac{3}{2}\right\}\)
a.\(m=-3\Rightarrow x^2-2\left(-3-1\right)x-\left(-3\right)-3=0\)
\(\Leftrightarrow x^2+8x=0\\ \Leftrightarrow x\left(x+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\)
b.
\(\Delta'=\left(m-1\right)^2-\left(-m-3\right)\\ =m^2-2m+1+m+3\)
\(=m^2-m+4\\ =\left(m-\dfrac{1}{2}\right)^2+\dfrac{15}{4}>\forall m\)
viết \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-m-3\end{matrix}\right.\)
ta có \(x_1^2+x_2^2=0\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)
\(\Leftrightarrow4\left(m-1\right)^2-2\left(-m-3\right)=10\)
\(\Leftrightarrow4\left(m^2-2m+1\right)+2m+6=10\\ \Leftrightarrow4m^2-6m=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{2}\\m=0\end{matrix}\right.\)
a) Thay m=-3 vào phương trình, ta được:
\(x^2+8x-\left(-3\right)-3=0\)
\(\Leftrightarrow x^2+8x=0\)
\(\Leftrightarrow x\left(x+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\)
b) Ta có: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot1\cdot\left(-m-3\right)\)
\(=\left(2m-1\right)^2+4\left(m+3\right)\)
\(=4m^2-4m+1+4m+12\)
\(=4m^2+13>0\forall m\)
Do đó: Phương trình luôn có hai nghiệm phân biệt với mọi m
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-m-3\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=10\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)
\(\Leftrightarrow\left(2m-2\right)^2-2\left(-m-3\right)-10=0\)
\(\Leftrightarrow4m^2-8m+4+2m+6-10=0\)
\(\Leftrightarrow4m^2-6m=0\)
\(\Leftrightarrow2m\left(2m-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{3}{2}\end{matrix}\right.\)