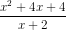a) Để phân thức được xác định thì
x3-8\(\ne\)0
<=> (x-2)(x2+2x+4)\(\ne\) 0
\(< =>\left[\begin{matrix}x-2\ne0\\x^2+2x+4\ne0\end{matrix}\right.\Leftrightarrow\left[\begin{matrix}x\ne2\\x^2+2x+4>0\end{matrix}\right.\)
Vậy ĐKXĐ x\(\ne\)2
b)\(\frac{3x^2+6x+12}{x^3-8}=\frac{3\left(x^2+2x+4\right)}{\left(x-2\right)\left(x^2+2x+4\right)}=\frac{3}{x-2}\)
c) Với x = \(\frac{4001}{2000}\) thì \(\frac{3}{\frac{4001}{2000}-2}\) =6000
CHÚC BẠN HỌC TỐT!!
a) Điều kiện các định khi \(x^3-8\ne0\)
\(\Rightarrow\left(x-2\right)\left(x^2+2x+4\right)\ne0\)
\(\Rightarrow\left[{}\begin{matrix}x-2\ne0\\x^2+2x+4\ne0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x\ne2\\\left(x+1\right)^2+3>0\left(loai\right)\end{matrix}\right.\)
\(\Rightarrow\) điều kiện xác định khi \(x\ne2\)
b) \(\dfrac{3x^2+6x+12}{x^3-8}\)
\(=\dfrac{3\left(x^2+2x+4\right)}{\left(x-2\right)\left(x^2+2x+4\right)}\)
\(=\dfrac{3}{x-2}\)
c) Thay \(x=\dfrac{4001}{2000}\) vào biểu thức trên ta được:
\(\dfrac{3}{\dfrac{4001}{2000}-2}\)
\(=\dfrac{3}{\dfrac{4001}{2000}-\dfrac{4000}{2000}}\)
\(=\dfrac{3}{\dfrac{4001-4000}{2000}}\)
\(=\dfrac{3}{\dfrac{1}{2000}}\)
\(=6000\)
Vậy giá trị của biểu trên tại \(x=\dfrac{4001}{2000}\) là \(6000\)
a) Để phân thức được xát định thì:
x3- 8\(\ne\) 0 hay x3- 23\(\ne\) 0
=> (x - 2)(x2 + 2x + 4)\(\ne\) 0
=> x - 2 \(\ne\) 0 và (x + 2)2\(\ne\) 0
=> \(\left[\begin{matrix}x-2\\x+2\end{matrix}\right.\)\(\ne\) 0 => x\(\ne\) 2 và x\(\ne\) -2
Vậy ĐKXĐ: x\(\ne\)\(\pm\) 2
b) \(\frac{3x^2+6x+12}{x^3-8}\) = \(\frac{3\left(x^2+2x+4\right)}{\left(x-2\right)\left(x^2+2x+4\right)}\)
= \(\frac{3}{x-2}\)
c) Thay x = \(\frac{4001}{2000}\) vào phân thức sau khi rút gọn là \(\frac{3}{x-2}\) ta được:
\(\frac{3}{x-2}\) = \(\frac{3}{\frac{4001}{2000}-2}\)
= \(\frac{3}{\frac{4001}{2000}-\frac{2}{1}}\) = \(\frac{3}{\frac{4001-4000}{2000}}\)
= \(\frac{3}{\frac{1}{2000}}\) = 3: \(\frac{1}{2000}\)
= \(\frac{3.2000}{1}\) = \(\frac{6000}{1}\) = 6000
Vậy phân thức có giá trị là 6000 khi x = \(\frac{4001}{2000}\)
XONG RỒI ![]()
( bài này mình giải rất chi tiết đó )![]()