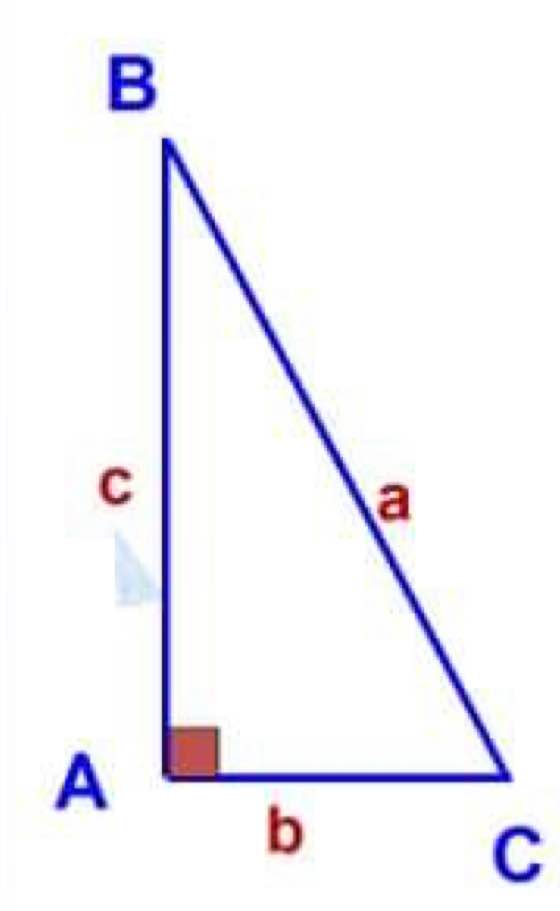
Xét ΔKMN vuông tại K có
\(\sin\widehat{M}=\frac{KN}{MN}\); \(\cos\widehat{M}=\frac{KM}{MN}\);
\(\tan\widehat{M}=\frac{KN}{KM}\); \(\cot\widehat{M}=\frac{KM}{KN}\)
Ta có: ΔKMN vuông tại K(gt)
\(\Rightarrow\widehat{M}+\widehat{N}=90^0\)(hai góc phụ nhau)
\(\Rightarrow\left\{{}\begin{matrix}\sin\widehat{M}=\cos\widehat{N}\\\cos\widehat{M}=\sin\widehat{N}\\\tan\widehat{M}=\cot\widehat{N}\\\cot\widehat{M}=\tan\widehat{N}\end{matrix}\right.\)(Tính chất tỉ số lượng giác góc nhọn)
\(\Rightarrow\sin\widehat{N}=\frac{KM}{MN}\); \(\cos\widehat{N}=\frac{KN}{MN}\);
\(\tan\widehat{N}=\frac{KM}{KN}\); \(\cot\widehat{N}=\frac{KN}{KM}\)