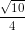Cho hình vuông \(C_1\) có cạnh bằng 4. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông \(C_2\) (h44). Từ hình vuông \(C_2\) lại tiếp như trên để được hình vuông \(C_3\),.......Tiếp tục quá trình như trên, ta nhận được dãy các hình vuông \(C_1,C_2,C_3,.....C_n,....\)
Gọi \(a_n\) là độ dài cạnh của hình vuông \(C_n\). Chứng minh dãy dố \(\left(a_n\right)\) là một cấp số nhân ?

Xét dãy số (an), ta có a1 = 4.
Giả sử hình vuông cạnh Cn có độ dài cạnh là an. Ta sẽ tính cạnh an+1 của hình vuông Cn+1. Theo hình 9, áp dụng định lí Pi-ta-go, ta có:
an+1 = 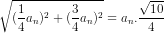 với n ε N*.
với n ε N*.
Vậy dãy số (an) là cấp số nhân với số hạng đầu là a1 = 4 và công bội q =