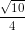Chứng minh các dãy số \(\left(\dfrac{3}{5}.2^n\right),\left(\dfrac{5}{2^n}\right),\left(\left(-\dfrac{1}{2}\right)^n\right)\) là các cấp số nhân ?
Bài 4: Cấp số nhân
Bài 1 (SGK trang 103)
Thảo luận (1)
Bài 2 (SGK trang 103)
Cho cấp số nhân \(\left(u_n\right)\) với công bội q.
a) Biết \(u_1=2;u_6=486\). Tìm q ?
b) Biết \(q=\dfrac{2}{3};u_4=\dfrac{8}{21}\). Tìm \(u_1\) ?
c) Biết \(u_1=3;q=-2\). Hỏi 192 là số hạng thứ mấy ?
Thảo luận (2)Hướng dẫn giảiTrong bài này ta áp dụng công thức tinh số hạng tổng quát un = u1.qn-1, biết hai đại lượng, ta sẽ tìm đại lượng còn lại:
a) q = 3.
b) u1 =
c) Theo đề bài ta có un = 192, từ đó ta tìm được n. Đáp số: n =7
(Trả lời bởi Đặng Phương Nam)
Bài 3 (SGK trang 103)
Tìm các số hạng của cấp số nhân \(\left(u_n\right)\) có năm số hạng, biết :
a) \(u_3=3\) và \(u_5=27\)
b) \(u_4-u_2=25\) và \(u_3-u_1=50\)
Thảo luận (1)Hướng dẫn giảia) Áp dụng công thức tính số hạng tổng quát, ta có:
u3 = 3 = u1.q2 và u5 = 27 = u1.q4.
Vì 27 = (u1q2).q2 = 3.q2 nên q2 = 9 hay q = ±3.
Thay q2 = 9 vào công thức chứa u3, ta có u1 =
.
- Nếu q = 3, ta có cấp số nhân:
, 1, 3, 9, 27.
- Nếu q = -3, ta có cáp số nhân:
, -1, 3, -9, 27.
b) Áp dụng công thức tính số hạng tỏng quát từ giả thiết, ta có:
hay

Từ hệ trên ta được: 50.q = 25 => q =
.
Và u1 =
.
Ta có cấp số nhân
.
(Trả lời bởi Minh Hải)
Bài 4 (SGK trang 104)
Tìm cấp số nhân có 6 số hạng, biết rằng tổng của năm số hạng đầu là 31 và tổng của năm số hạng sau là 62 ?
Thảo luận (1)Hướng dẫn giảiGiả sử có cấp số nhân: u1, u2, u3, u4, u5,u6.
Theo giả thiết ta có:
u1 + u2 + u3 + u4 + u5 = 31. (1)
và u2 + u3 + u4 + u5 + u6 = 62. (2)
Nhân hai vế của (1) với q, ta được: q.u1 + q.u2 + q.u3 +q. u4 +q. u5 = 31.q
hay u2 + u3 + u4 + u5 + u6 = 31q
Suy ra 62 = 31.q hay q = 2.
Ta có S5 = 31 =
nên suy ra u1 = 1.
Vậy ta có cấp số nhân 1, 2, 4, 8, 16, 32.
(Trả lời bởi Đặng Phương Nam)
Bài 5 (SGK trang 104)
Tỉ lệ tăng dân số của tỉnh X là 1,4%. Biết rằng số dân của hiện nay là 1,8 triệu người. Hỏi với mức tăng như vậy thì sau 5 năm, 10 năm số dân của tỉnh đó là bao nhiêu ?
Thảo luận (1)Hướng dẫn giảiGiả sử số dân của một tỉnh đó hiện nay là N. Vì tỉ lệ tăng dân số là 1,4% nên sau một năm, số dân tăng thêm là 1,4%.N
Vậy số dân của tỉnh đó vào năm sau là
N + 1,4%.N = 101,4%.N =
.
Như vậy số dân của tỉnh đó sau mỗi năm lập thành cấp số nhân.
N,
,
, ....
Vậy nếu N = 1,8 triệu người, áp dụng công thức tính số hạng tổng quát của cấp số nhân thì sau 5 năm số dân của tỉnh là
≈ 1,9 (triệu người)
và sau 10 năm sẽ là
≈ 2,1 (triệu người)
(Trả lời bởi Minh Hải)
Bài 6 (SGK trang 104)
Cho hình vuông C_1 có cạnh bằng 4. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C_2 (h44). Từ hình vuông C_2 lại tiếp như trên để được hình vuông C_3,.......Tiếp tục quá trình như trên, ta nhận được dãy các hình vuông C_1,C_2,C_3,.....C_n,....
Gọi a_n là độ dài cạnh của hình vuông C_n. Chứng minh dãy dố left(a_nright) là một cấp số nhân ?
Đọc tiếp
Cho hình vuông \(C_1\) có cạnh bằng 4. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông \(C_2\) (h44). Từ hình vuông \(C_2\) lại tiếp như trên để được hình vuông \(C_3\),.......Tiếp tục quá trình như trên, ta nhận được dãy các hình vuông \(C_1,C_2,C_3,.....C_n,....\)
Gọi \(a_n\) là độ dài cạnh của hình vuông \(C_n\). Chứng minh dãy dố \(\left(a_n\right)\) là một cấp số nhân ?

Thảo luận (1)Hướng dẫn giảiXét dãy số (an), ta có a1 = 4.
Giả sử hình vuông cạnh Cn có độ dài cạnh là an. Ta sẽ tính cạnh an+1 của hình vuông Cn+1. Theo hình 9, áp dụng định lí Pi-ta-go, ta có:
an+1 =
với n ε N*.
Vậy dãy số (an) là cấp số nhân với số hạng đầu là a1 = 4 và công bội q =
(Trả lời bởi Minh Hải)
Bài 4.1 (Sách bài tập trang 125)
Cho dãy số \(\left(u_n\right)=\left(-3\right)^{2n-1}\)
a) Chứng minh dãy số \(\left(u_n\right)\) là cấp số nhân. Nêu nhận xét về tính tăng, giảm của dãy số
b) Lập công thức truy hồi của dãy số
c) Hỏi số -19683 là số hạng thứ mấy của dãy số ?
Thảo luận (1)Hướng dẫn giảia) Có \(u_n=\left(-3\right)^{2n-1}=\left(-3\right)^2.\left(-3\right)^{2n-3}\)\(=9.2^{2\left(n-1\right)-1}=9.u_{n-1}\)
(Trả lời bởi Bùi Thị Vân)
Vì vậy \(\left(u_n\right)\) là dãy số nhân với \(u_1=\left(-3\right)^{2.1-1}=-3\) và \(q=9\).
b) Công thức truy hồi của dãy số \(\left(u_n\right)\) là \(u_n=9u_{n-1}\).
c) Có \(u_n=\left(-3\right)^{2n-1}=-19683=\left(-3\right)^9\)\(\Leftrightarrow2n-1=9\)\(\Leftrightarrow n=5\).
Vậy số hạng thứ 5 bằng \(-19683\).
Bài 4.2 (Sách bài tập trang 125)
Cấp số nhân \(\left(u_n\right)\) có
\(\left\{{}\begin{matrix}u_1+u_5=51\\u_2+u_6=102\end{matrix}\right.\)
a) Tìm số hạng đầu và công bội của cấp số nhân ?
b) Hỏi tổng của bao nhiêu số hạng đầu tiên sẽ bằng 3069 ?
c) Số 12 288 là số hạng thứ mấy ?
Thảo luận (1)Hướng dẫn giảia)
(Trả lời bởi Bùi Thị Vân)
Gọi q là công bội của \(\left(u_n\right)\). Ta có:
\(\left\{{}\begin{matrix}u_1+u_1q^4=51\\u_1q+u_1q^5=102\end{matrix}\right.\)\(\Rightarrow\dfrac{u_1+u_1q^4}{u_1q_1+u_1q^5}=\dfrac{51}{102}\)\(\Leftrightarrow\dfrac{1+q^4}{q+q^5}=\dfrac{1}{2}\)\(\Leftrightarrow\dfrac{1+q^4}{q\left(1+q^4\right)}=\dfrac{1}{2}\)\(\Leftrightarrow\dfrac{1}{q}=\dfrac{1}{2}\)\(\Leftrightarrow q=2\).
Suy ra: \(u_1+2^4u_1=51\)\(\Leftrightarrow17u_1=51\)\(\Leftrightarrow u_1=3\).
b) \(S_n=\dfrac{u_1\left(1-q^n\right)}{1-q}=\)\(\dfrac{3\left(1-2^n\right)}{1-2}=3\left(2^n-1\right)=3069\)
\(\Leftrightarrow2^n-1=1023\)\(\Leftrightarrow2^n=1024=2^{10}\)\(\Leftrightarrow n=10\).
Vậy tổng của 10 số hạng đầu tiên bằng 10.
c)
Có \(u_1.q^{n-1}=3.2^{n-1}=12288\)\(\Leftrightarrow2^{n-1}=4096=2^{12}\)\(\Leftrightarrow n-1=12\)\(\Leftrightarrow n=13\).
Vậy số hạng thứ 13 bằng 12 288.
Bài 4.3 (Sách bài tập trang 125)
Tìm số các số hạng của cấp số nhân \(\left(u_n\right)\) biết :
a) \(q=2\) \(u_n=96\) \(S_n=189\)
b) \(u_1=2\) \(u_n=\dfrac{1}{8}\) \(S_n=\dfrac{31}{8}\)
Thảo luận (1)Hướng dẫn giảia) \(u_n=u_1.q^{n-1}=u_1.2^{n-1}\)
(Trả lời bởi Bùi Thị Vân)
\(S_n=\dfrac{u_1\left(1-q^n\right)}{1-q}=\dfrac{u_1\left(1-2^n\right)}{1-2}=u_1\left(2^n-1\right)\);
\(\dfrac{S_n}{u_n}=\dfrac{u_1\left(2^n-1\right)}{u_1.2^{n-1}}=\dfrac{2^n-1}{2^{n-1}}=2-\dfrac{1}{2^{n-1}}=\dfrac{63}{32}\)
Vì vậy \(\dfrac{1}{2^{n-1}}=\dfrac{1}{32}\) \(\Leftrightarrow\dfrac{1}{2^{n-1}}=\dfrac{1}{2^5}\)\(\Leftrightarrow n-1=5\Leftrightarrow n=6\).
b)
\(u_n=2.q^{n-1}=\dfrac{1}{8}\)\(\Rightarrow q^{n-1}=\dfrac{1}{16}\)
\(S_n=\dfrac{2\left(1-q^n\right)}{1-q}=\dfrac{2\left(1-q.q^{n-1}\right)}{1-q}=\dfrac{2\left(1-\dfrac{1}{16}q\right)}{1-q}=\dfrac{31}{8}\);
Suy ra \(q=-1\).
Bài 4.4 (Sách bài tập trang 125)
Tìm số hạng đầu và công bội của cấp số nhân \(\left(u_n\right)\) biết :
a) \(\left\{{}\begin{matrix}u_5-u_1=15\\u_4-u_2=6\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}u_2-u_4+u_5=10\\u_3-u_5+u_6=20\end{matrix}\right.\)
Thảo luận (1)Hướng dẫn giảiGọi số hạng đầu và công bội của cấp số nhân là: \(u_1;q\).
(Trả lời bởi Bùi Thị Vân)
a) Theo tính chất của cấp số nhân ta có:
\(\left\{{}\begin{matrix}u_1q^4-u_1=15\\u_1q^3-u_1q=6\end{matrix}\right.\)\(\Rightarrow\dfrac{u_1\left(q^4-1\right)}{u_1\left(q^3-q\right)}=\dfrac{15}{6}\)\(\Leftrightarrow\dfrac{\left(q^2-1\right)\left(q^2+1\right)}{q\left(q^2-1\right)}=\dfrac{15}{6}\)\(\Leftrightarrow\dfrac{q^2+1}{q}=\dfrac{15}{6}\)
\(\Leftrightarrow6\left(q^2+1\right)=15q\)\(\Leftrightarrow6q^2-15q+6=0\)\(\Leftrightarrow\left[{}\begin{matrix}q=2\\q=\dfrac{1}{2}\end{matrix}\right.\).
Với \(q=2\).
Suy ra: \(u_1\left(q^4-q\right)=15\Rightarrow u_1=\dfrac{15}{q^4-q}=\dfrac{15}{14}\).
Với \(q=\dfrac{1}{2}\)
Suy ra \(u_1=\dfrac{15}{q^4-q}=\dfrac{-240}{7}\).