https://hoc24.vn/hoi-dap/question/18469.html
tham khảo đi bạn
giống đó
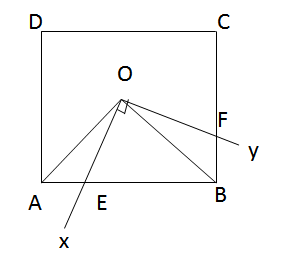
Nối OA,OBOA,OB. Hai tam giác AOEAOE và BOFBOF có:
ˆAOE=ˆBOFAOE^=BOF^ (cùng phụ với ˆBOEBOE^)
OA=OBOA=OB (O là tâm đối xứng của hình vuông)
ˆOAE=ˆOBF=450OAE^=OBF^=450 (tính chất hình vuông)
Nên ΔAOE=ΔBOF(g−c−c)
Do đó
SOBEF=SOEB+SOBF=SOEB+SOAE=SOAB
Vậy SOEFB=\(\dfrac{1}{2}\)SABCD=\(\dfrac{1}{4}\)a2
Mik làm lại cho đủ:
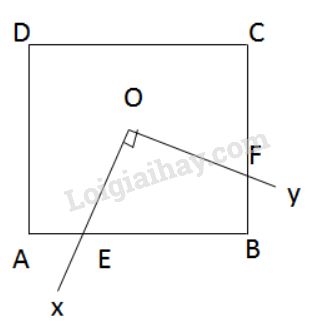
Nối OA,OBOA,OB. Hai tam giác AOE và BOF có:
\(\widehat{AOE}\)=\(\widehat{BOF}\) (cùng phụ với \(\widehat{BOE}\))
OA=OB (O là tâm đối xứng của hình vuông)
\(\widehat{OAE}\) =\(\widehat{OBF}\)=45o (tính chất hình vuông)
Nên ΔAOE=ΔBOF(g−c−c)
Do đó SOEBF=SOEB+SOBF=SOEB+SOAE=SOAB
Vậy SOEBF=\(\dfrac{1}{4}\)SABCD=\(\dfrac{1}{4}\)a2














