Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
Các câu hỏi tương tự
Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 25 cm, HC = 64 cm. Tính góc B và góc C ?
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
Tính diện tích hình thang cân, biết hai cạnh đáy là 12 cm và 18 cm, góc ở đáy bằng \(75^0\) ?
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
Bài 8. Cho AABC vuông tại A có AB = 5cm; BC = 13cm; AH là đường cao. a) Tính AC, AH và B ( Số đo góc làm tròn đến độ, độ dài cạnh làm tròn đến chữ số thì phân thứ hai ). b) Gọi E, F lần lượt là hình chiếu của H trên AB, AC. Chứng minh AE.EB+AF.FC- HB.HC=0 c) Chứng minh AH=EF. Từ đó suy ra BC =3AH + BE +CF.
Tính diện tích các hình bình hành có hai cạnh 12cm và 15 cm, góc tạo bởi hai cạnh ấy bằng \(110^0\) ?
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
Cho tam giác ABC có \(BC=12cm,\widehat{B}=60^0,\widehat{C}=40^0\). Tính :
a) Đường cao CH và cạnh AC
b) Diện tích tam giác ABC
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
Tam giác ABC vuông tại A có \(AB=21cm,\widehat{C}=40^0\). Hãy tính các độ dài :
a) AC
b) BC
c) Phân giác BD
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
Bài 2: Cho tam giác ABC nhọn có đường cao AH. Gọi E là hình chiếu của H trên AB.a, Biết AE 3,6 cm ; BE 6,4 cm. Tính AH, EH và góc B ( Số đo góc làm tròn đến độ)b, Kẻ HF vuông góc với AC tại F. Chứng minh AB . AE AC . AFc , Đường thẳng qua A và vuông góc với EF cắt BC tại D; EF cắt AH tại O. C1, Chứng minh tam giác AEF đồng dạng với tam giác ACB C2, Chứng minh:
Đọc tiếp
Bài 2: Cho tam giác ABC nhọn có đường cao AH. Gọi E là hình chiếu của H trên AB.
a, Biết AE = 3,6 cm ; BE = 6,4 cm. Tính AH, EH và góc B ( Số đo góc làm tròn đến độ)
b, Kẻ HF vuông góc với AC tại F. Chứng minh AB . AE = AC . AF
c , Đường thẳng qua A và vuông góc với EF cắt BC tại D; EF cắt AH tại O.
C1, Chứng minh tam giác AEF đồng dạng với tam giác ACB
C2, Chứng minh:
Cho hình 16.
Biết ABAC8cm,CD6cm,widehat{BAC}34^0,widehat{CAD}42^0. Hãy tính :
a) Độ dài cạnh BC
b) widehat{ADC}
c) Khoảng cách từ điểm B đến cạnh AD
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
Đọc tiếp
Cho hình 16.
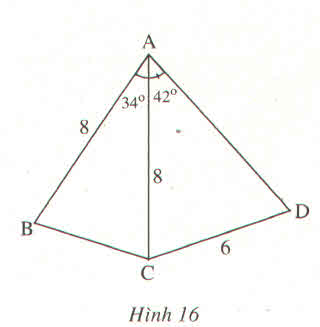
Biết \(AB=AC=8cm,CD=6cm,\widehat{BAC}=34^0,\widehat{CAD}=42^0\). Hãy tính :
a) Độ dài cạnh BC
b) \(\widehat{ADC}\)
c) Khoảng cách từ điểm B đến cạnh AD
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
Bài 4. Cho đường tròn tâm O, đường kính AB = 10 cm và điểm C thuộc đường tròn sao cho AC=6 cm. Về CH vuông góc với AB tại H.
a) Chứng minh rằng tam giác ABC vuông tại C.
b) Tính HB và HC.
c) Trên tia đối của tia CA lấy điểm D sao cho CD= 2 cm. Gọi M là giao điểm của BD với đường tròn(M khác B). Chứng minh rằng CMD = CAB.





