Question

Cho hình tam giác ABC, góc A = 80 độ, góc B = 50 độ. Trên tia đối của tia AB lấy điểm O. Trên nửa mp ko chứa điểm c. Bờ là đường thẳng AB ta vẽ tia Ox, sao cho góc BÕ = 50 độ. Gọi tia Ay là tia pg của góc cAO. CMR : Ox // Ay ; Ay // CB; Ox // CB

Answer 1

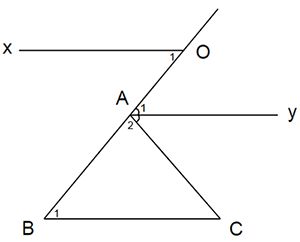
Ta có: \(\widehat{B}=\widehat{BOx}=50^0\left(gt\right)\)

Mà 2 góc này nằm ở vị trí so le trong

=> \(Ox\) // \(BC.\)

Lại có: \(\widehat{CAB}+\widehat{OAC}=180^0\) (vì 2 góc kề bù)

=> \(80^0+\widehat{OAC}=180^0\)

=> \(\widehat{OAC}=180^0-80^0\)

=> \(\widehat{OAC}=100^0.\)

Mà \(Ay\) là tia phân giác của \(\widehat{OAC}\left(gt\right)\)

=> \(\widehat{CAy}=\widehat{yAO}=\frac{\widehat{OAC}}{2}=\frac{100^0}{2}=50^0.\)

Xét \(\Delta ABC\) có:

\(\widehat{A}+\widehat{B}+\widehat{ACB}=180^0\) (định lí tổng 3 góc trong một tam giác)

=> \(80^0+50^0+\widehat{ACB}=180^0\)

=> \(130^0+\widehat{ACB}=180^0\)

=> \(\widehat{ACB}=180^0-130^0\)

=> \(\widehat{ACB}=50^0.\)

=> \(\widehat{CAy}=\widehat{ACB}=50^0\)

Mà 2 góc này nằm ở vị trí so le trong

=> \(Ay\) // \(BC.\)

Mà \(Ox\) // \(BC\left(cmt\right)\)

=> \(Ox\) // \(Ay.\)

Chúc bạn học tốt!