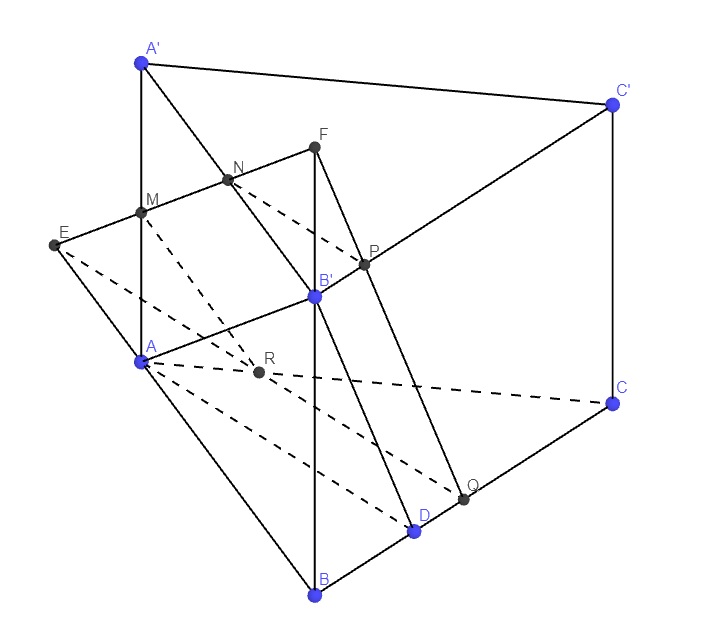
Em tự thực hiện việc dựng hình, khá đơn giản chỉ mấy đường song song
Theo t/c giao tuyến của 3 mp cắt nhau ta có AP, QR và MN đồng quy tại 1 điểm. Gọi điểm đó là E.
MN, BB', PQ đồng quy tại 1 điểm. Gọi điểm đó là F.
Hai tam giác B'AD và FEQ đồng dạng (3 cặp cạnh song song)
Các tứ giác AMFB' và AENB' là hình bình hành (các cặp cạnh đối song song)
\(\Rightarrow MF=AB'=NE\Rightarrow ME=NF\)
Do MN là đường trung bình tam giác A'AB' \(\Rightarrow MN=\dfrac{1}{2}AB'\Rightarrow MN=ME=MF=\dfrac{1}{2}AB'\)
\(\Rightarrow EF=\dfrac{3}{2}AB'\)
\(\Rightarrow\) 2 tam giác B'AD và FEQ đồng dạng theo tỉ số \(\dfrac{EF}{AB'}=\dfrac{3}{2}\)
\(\Rightarrow S_{FEQ}=\left(\dfrac{3}{2}\right)^2S_{B'AD}=\dfrac{9}{4}S_{B'AD}\)
\(\dfrac{AD}{EQ}=\dfrac{AB'}{EF}=\dfrac{2}{3}=\dfrac{BD}{BQ}\) \(\Rightarrow BQ=\dfrac{3}{2}BD=\dfrac{3}{2}.\dfrac{1}{3}BC=\dfrac{1}{2}BC\)
Menelaus tam giác BEQ:
\(\dfrac{RE}{RQ}.\dfrac{QC}{CB}.\dfrac{BA}{AE}=1\Rightarrow\dfrac{RE}{RQ}.\dfrac{1}{2}.2=1\Rightarrow RE=RQ\Rightarrow RE=\dfrac{1}{2}EQ\)
\(\Rightarrow S_{MER}=\dfrac{ME}{FE}.\dfrac{RE}{EQ}.S_{FEQ}=\dfrac{1}{3}.\dfrac{1}{2}=\dfrac{1}{6}S_{FEQ}\)
\(\Delta FNP\) đồng dạng \(\Delta FEQ\) (do NP song song EQ) theo tỉ số đồng dạng \(\dfrac{NF}{EF}=\dfrac{1}{3}\)
\(\Rightarrow S_{FNP}=\dfrac{1}{9}S_{FEQ}\)
\(\Rightarrow S_{MNPQR}=S_{FEQ}-\left(S_{FNP}+S_{MER}\right)=\dfrac{13}{18}S_{FEQ}=\dfrac{9}{4}.\dfrac{13}{18}S_{B'AD}=\dfrac{13}{8}S_{B'AD}\)