Ôn tập chương II - Đa giác. Diện tích đa giác
Các câu hỏi tương tự
Cho hình thang ABCD (AB//CD); E là trung điểm của AD. Gọi H là hình chiếu của E trên đường thẳng CD. Qua E, vẽ đường thẳng song song với BC, cắt đường thẳng AB và CD lần lượt tại I và K. Cho biết EH = 5 cm, BC = 8 cm; tính diện tích tứ giác IBCK, ABC...
Xem chi tiết
Cho tam giác ABD vuông tại A có AB <AD . M là trung điểm của BD . GọiC là điểm đối xứng với A qua M
a, CM tứ giác ABCD là hình chữ nhật
b, Trên tia đối của tia DA lấy E sao cho DE=DA. Gọi I là trung điểm của CD CM: IB=IE
c, gọi AH là đường cao của tam giác ABD và K là điểm đối xứng với A qua H. CM: tứ giác BDCK là hình thang cân
d , chứng minh rằng k,C,E thẳng hàng
Cho HBH ABCD có AC vuông góc với AD . Gọi E,F theo thứ tự là trung điểm của AB và CD .
a, Tứ giác AECF là hình gì ? Vì sao?
b, Cm CA là tia phân giác của góc ECF .
c, Giả sử HBH ABCD có CD=5 cm . Hãy tính chu vi của tứ giác AECF .
Xem chi tiết
Cho tứ giác ABCD. Hai đường chéo AC và BD vuông góc với nhau. Gọi E, F, G và H lần lượt là trung điểm của các cạnh AB, BC, CD và DA
a) chứng minh tứ giác EFGH là hình chữ nhật
b) biết AC=10cm, BD=8cm. Tính diện tích tứ giác EFGH
c) Để EFGH là hình vuông thì tứ giác ABCD cần có thêm điều kiện gì về hai đường chéo ?
Xem chi tiết
Bài 2: Cho hình bình hành ABCD có CD = 16 cm, đường cao vẽ từ A đến cạnh CD bằng 12 cm. \
a,Tính diện tích hình bình hành ABCD.
b,Gọi M là trung điểm AB, Tính diện tích tam giác ADM.
c,DM cắt AC tại N. Chứng minh rằng DN= 2NM
d, Tính diện tích tam giác AMN.
Cho hình chữ nhật ABCD. Gọi H, I, E, K lần lượt là các trung điểm của BC, HC, DC, EC (h.159)
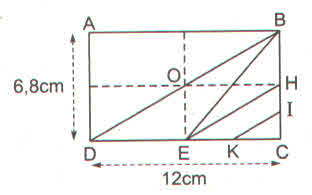
Tính :
a) Diện tích tam giác DBE
b) Diện tích tứ giác EHIK
28 tháng 12 2017 lúc 20:02
Cho tứ giác lồi ABCD có AB và CD kéo dài tạo thành một góc vuông. Gọi M,N,P,Q theo thứ tự là trung điềm của BC, BD,Ad và AC.
-Chứng minh MNPQ là hình chữ nhật.
- Nếu cho thêm điều kiện BC// AD, BC=4cm, AD= 16cm thì độ dài MP bằng bao nhiều?
Các bạn giúp mình nha! Cảm ơn nhiều nha!
Cho tam giác ABC có M là TĐ AC, N là TĐ AB, E TĐ BC
a. C/M ABCD là HBH
b. CM A,D,K thẳng hàng
c. Gọi I là giao điểm của AE với BM . C/M diện tích tam giác AIB=1/6 diện tích ABCD
1/Cho hình thoi ABCD .Gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O không song song với AD cắt AB tại M và CD tại N
a)CM:△AOM △CON
b)Chứng tỏ tứ giác AMCN là hình bình hành
2/Cho hình chữ nhật ABCD có AB6cm, AC10cm.Gọi O là giao điểm hai đường chéo AC và BD và M, N, P, Q lần lượt là trung điểm của OA, OB, OC, OD
a)Tính SMNPQ
b) CM rằng :SAMNBSCPQD
Đọc tiếp
1/Cho hình thoi ABCD .Gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O không song song với AD cắt AB tại M và CD tại N
a)CM:△AOM =△CON
b)Chứng tỏ tứ giác AMCN là hình bình hành
2/Cho hình chữ nhật ABCD có AB=6cm, AC=10cm.Gọi O là giao điểm hai đường chéo AC và BD và M, N, P, Q lần lượt là trung điểm của OA, OB, OC, OD
a)Tính SMNPQ
b) CM rằng :SAMNB=SCPQD