Question

Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA và CD.

a) Chứng minh (OMN) // (SBC).

b) Giả sử hai tam giác SAD và ABC là các tam giác cân tại A. Gọi AE và AF lần lượt là đường phân giác trong của hai tam giác ACD và SAB. Chứng minh EF // (SAD).

Answer 1

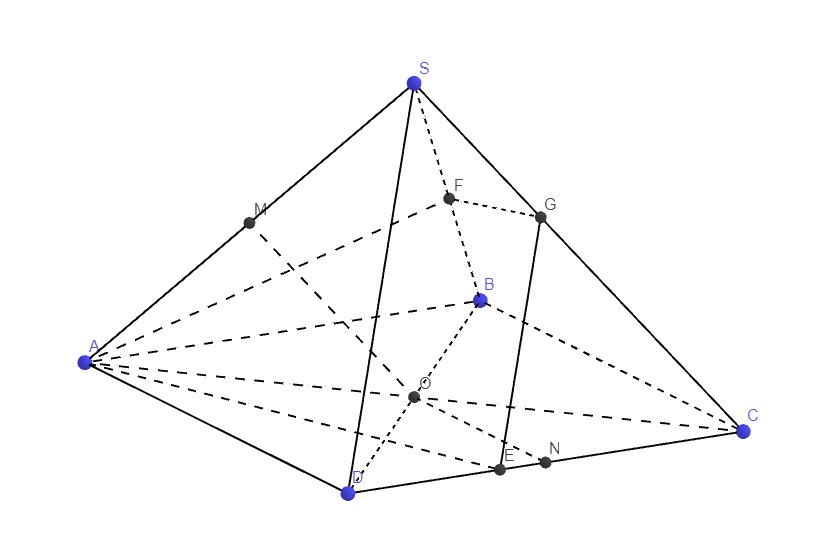
a.

O là trung điểm BD, N là trung điểm CD

\(\Rightarrow\) ON là đường trung bình tam giác BCD

\(\Rightarrow ON||BC\Rightarrow ON||\left(SBC\right)\)

Tương tự ta có OM là đtb tam giác SAC \(\Rightarrow OM||SC\Rightarrow OM||\left(SBC\right)\)

\(\Rightarrow\left(OMN\right)||\left(SBC\right)\)

b.

Trong mp (SCD), qua E kẻ đường thẳng song song SD cắt SC tại G

\(\Rightarrow EG||SD\Rightarrow EG||\left(SAD\right)\) (1)

Theo định lý Talet: \(\dfrac{EC}{ED}=\dfrac{GC}{GS}\)

Mặt khác AE là phân giác của ACD nên theo định lý phân giác: \(\dfrac{EC}{ED}=\dfrac{AC}{AD}\)

Mà ABC cân tại A \(\Rightarrow AB=AC\); SAD cân tại A \(\Rightarrow AD=SA\)

\(\Rightarrow\dfrac{GC}{GS}=\dfrac{EC}{ED}=\dfrac{AC}{AD}=\dfrac{AB}{SA}\)

AF là phân giác nên áp dụng định lý phân giác:

\(\dfrac{FB}{FS}=\dfrac{AB}{SA}\) \(\Rightarrow\dfrac{FB}{FS}=\dfrac{GC}{GS}\Rightarrow FG||BC\) (Talet đảo) 

\(\Rightarrow FG||AD\Rightarrow FG||\left(SAD\right)\) (2)

(1);(2)  \(\Rightarrow\left(EFG\right)||\left(SAD\right)\Rightarrow EF||\left(SAD\right)\)

Answer 2