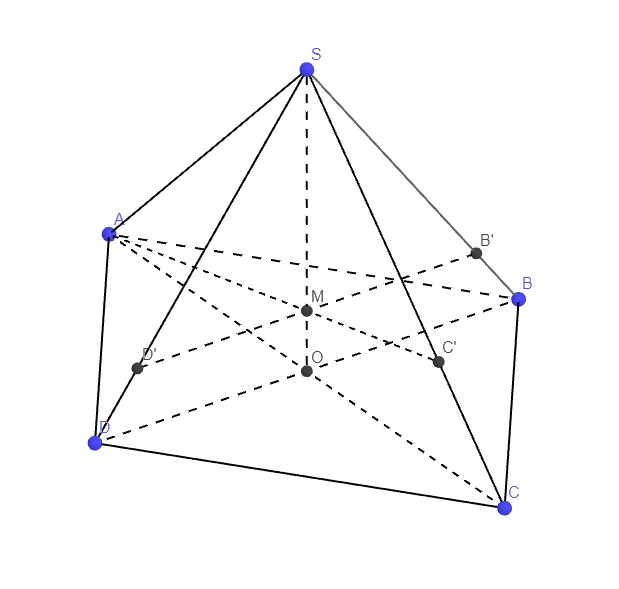
Cho hình chóp S.ABCD có đáy là hình bình hành. Lấy điểm M sao cho \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}+\overrightarrow{MS}=\overrightarrow{0}\) . Mặt phẳng đi qua AM cắt SB, SC, SD thứ tự tại B' C' D'. Tính \(\dfrac{BB'}{SB'}+\dfrac{CC'}{SC'}+\dfrac{DD'}{SD'}\)
Gọi O là giao điểm AC và BD, theo t/c hình bình hành \(\Rightarrow O\) là trung điểm AC và BD
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0}\\\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}\end{matrix}\right.\)
Từ giả thiết:
\(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}+\overrightarrow{MS}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OC}+\overrightarrow{MO}+\overrightarrow{OD}+\overrightarrow{MO}+\overrightarrow{OS}=\overrightarrow{0}\)
\(\Leftrightarrow5.\overrightarrow{MO}+\overrightarrow{OS}=0\)
\(\Leftrightarrow\overrightarrow{OM}=\dfrac{1}{5}\overrightarrow{OS}\)
Hay M là điểm thuộc đoạn thẳng OS sao cho \(OM=\dfrac{1}{5}OS\) \(\Rightarrow SM=4MO\)
Do M thuộc OS \(\Rightarrow M\in\left(SAC\right)\), kéo dài AM cắt SC tại \(C'\) \(\Rightarrow C'\) là điểm cố định (bất chấp vị trí mặt phẳng (P))
Áp dụng định lý Menelaus trong tam giác SOC với 3 điểm A, M, C' thẳng hàng:
\(\dfrac{MS}{MO}.\dfrac{OA}{AC}.\dfrac{CC'}{C'S}=1\Rightarrow4.\dfrac{1}{2}.\dfrac{CC'}{C'S}=1\Rightarrow\dfrac{CC'}{SC'}=\dfrac{1}{2}\)
Bây giờ tới B' và D'.
Cách đơn giản nhất là đề ko cho biết rõ về mp (P), nó chỉ cần chứa AM là đủ, do đó ta chọn vị trí đơn giản nhất của (P) để tính, đó là (P) song song BD. Khi đó, qua M kẻ đường thẳng song song BD lần lượt cắt SB, SD tại B' và D'
Theo định lý Talet:
\(\dfrac{BB'}{SB'}=\dfrac{DD'}{SD'}=\dfrac{MO}{SM}=\dfrac{1}{4}\)
\(\Rightarrow\dfrac{BB'}{SB'}+\dfrac{CC'}{SC'}+\dfrac{DD'}{SD'}=\dfrac{1}{4}+\dfrac{1}{2}+\dfrac{1}{4}=1\)
Trong trường hợp ko muốn làm kiểu chọn mp đặc biệt này thì ta có thể chọn vị trí bất kì cho B', nhưng sẽ tốn thời gian hơn nhiều. Nếu em cần thì cũng có thể giải quyết theo cách ấy.
Tổng quát:
Trước hết ta nhắc lại định lý đồng phẳng: cho 3 vecto \(\overrightarrow{a};\overrightarrow{b};\overrightarrow{c}\), chúng đồng phẳng khi và chỉ khi tồn tại các số thực m; n sao cho \(\overrightarrow{a}=m.\overrightarrow{b}+n.\overrightarrow{c}\) (1)
Bây giờ ta dựa vào đó chứng minh định lý khác về đồng phẳng trong không gian:
4 điểm A;B;C;D đồng phẳng khi \(\overrightarrow{SD}=p.\overrightarrow{SA}+m.\overrightarrow{SB}+n.\overrightarrow{SC}\) với 1 điểm S là 1 điểm bất kì và \(m;n;p\) là các số thực thỏa mãn \(m+n+p=1\)
C/m: do A;B;C;D đồng phẳng \(\Rightarrow\overrightarrow{AB};\overrightarrow{AC};\overrightarrow{AD}\) đồng phẳng
Theo (1), tồn tại các số thực m và n sao cho:
\(\overrightarrow{AD}=m.\overrightarrow{AB}+n.\overrightarrow{AC}\Leftrightarrow\overrightarrow{AS}+\overrightarrow{SD}=m\left(\overrightarrow{AS}+\overrightarrow{SB}\right)+n\left(\overrightarrow{AS}+\overrightarrow{SC}\right)\)
\(\Leftrightarrow\overrightarrow{SD}=m.\overrightarrow{SB}+n.\overrightarrow{SC}+\left(1-m-n\right).\overrightarrow{SA}\)
Đặt \(1-m-n=p\Rightarrow\left\{{}\begin{matrix}m+n+p=1\\\overrightarrow{SD}=m.\overrightarrow{SB}+n.\overrightarrow{SC}+p.\overrightarrow{SA}\end{matrix}\right.\) (đpcm)
Quay lại bài toán, ta tính toán cho trường hợp các điểm B' D' lần lượt nằm trên đoạn thẳng SB và SD (trường hợp có 1 điểm nằm ngoài tính y hệt).
Đặt \(\dfrac{SB}{SB'}=x;\dfrac{SC}{SC'}=y;\dfrac{SD}{SD'}=z\)
Do O là trung điểm AC và BD nên: \(\left\{{}\begin{matrix}\overrightarrow{SA}+\overrightarrow{SC}=2\overrightarrow{SO}\\\overrightarrow{SB}+\overrightarrow{SD}=2\overrightarrow{SO}\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=4\overrightarrow{SO}\)
\(\Rightarrow\overrightarrow{SA}+x.\overrightarrow{SB'}+y.\overrightarrow{SC'}+z.\overrightarrow{SD'}=5\overrightarrow{SM}\) (do \(\overrightarrow{SO}=\dfrac{5}{4}\overrightarrow{SM}\))
Do A;B'C'D' đồng phẳng nên tồn tại \(m+n+p=1\) sao cho \(\overrightarrow{SA}=m.\overrightarrow{SB'}+n.\overrightarrow{SC'}+p.\overrightarrow{SD'}\)
\(\Rightarrow\left(m+x\right)\overrightarrow{SB'}+\left(n+y\right)\overrightarrow{SC'}+\left(p+z\right)\overrightarrow{SD'}=5\overrightarrow{SM}\)
\(\Leftrightarrow\overrightarrow{SM}=\dfrac{1}{5}\left(m+x\right)\overrightarrow{SB'}+\dfrac{1}{5}\left(n+y\right)\overrightarrow{SC'}+\dfrac{1}{5}\left(p+z\right)\overrightarrow{SD'}\)
Do M;B'C'D' đồng phẳng nên:
\(\dfrac{1}{5}\left(m+x\right)+\dfrac{1}{5}\left(n+y\right)+\dfrac{1}{5}\left(p+z\right)=1\)
\(\Leftrightarrow m+n+p+x+y+z=5\)
\(\Leftrightarrow1+x+y+z=5\)
\(\Leftrightarrow x+y+z=4\)
\(\Leftrightarrow\dfrac{SB}{SB'}+\dfrac{SC}{SC'}+\dfrac{SD}{SD'}=4\)
\(\Leftrightarrow\dfrac{SB'+BB'}{SB'}+\dfrac{SC'+CC'}{SC'}+\dfrac{SD'+DD'}{SD'}=4\)
\(\Leftrightarrow\dfrac{BB'}{SB'}+\dfrac{CC'}{SC'}+\dfrac{DD'}{SD'}=1\)