Bài 1: Định lý Talet trong tam giác
Các câu hỏi tương tự
cho hình bình hành ABCD. một đường thẳng d cắt AB , BC, BD thứ tự tại M N I. chứng minh rằng : \(\dfrac{AB}{MB}+\dfrac{BC}{BN}=\dfrac{BD}{BI}\)
1 . Cho hình bình hành ABCD , qua D kẻ đường thẳng giao AC , AB , BC tại M , N , K . Cmr :
a . DM2 MN . MK
b . dfrac{1}{DN} + dfrac{1}{DK} dfrac{1}{DM}
2 . Cho hình bình hành ABCD , đường thẳng a cắt AB , BC và AC lần lượt tại E , F , M . Cmr :
dfrac{AB}{AE} + dfrac{AD}{AF} dfrac{AC}{AM}
Tớ cần gấp ạ : Làm 1 bài thôi cũng được :((
Đọc tiếp
1 . Cho hình bình hành ABCD , qua D kẻ đường thẳng giao AC , AB , BC tại M , N , K . Cmr :
a . DM2 = MN . MK
b . \(\dfrac{1}{DN}\) + \(\dfrac{1}{DK}\) = \(\dfrac{1}{DM}\)
2 . Cho hình bình hành ABCD , đường thẳng a cắt AB , BC và AC lần lượt tại E , F , M . Cmr :
\(\dfrac{AB}{AE}\) + \(\dfrac{AD}{AF}\) = \(\dfrac{AC}{AM}\)
Tớ cần gấp ạ :< Làm 1 bài thôi cũng được :((
Cho hình bình hành ABCD. Một đường thẳng qua A cắt tia đối tia BD tại I và cắt tia CB, CD tại H và K.
a) Chứng minh \(\dfrac{AH}{AK}=\dfrac{HB}{AD}\)
b) Hai tỉ số \(\dfrac{AH}{AK}\) và \(\dfrac{AH}{AI}\) bằng những tỉ số nào?
c) Chứng minh \(\dfrac{1}{AI}+\dfrac{1}{AK}=\dfrac{1}{AH}\)
Cho hình thang ABCD có AB //CD và AB CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
Chứng minh rằng :
a) dfrac{MA}{AD}dfrac{NB}{BC}
b) dfrac{MA}{MD}dfrac{NB}{NC}
c) dfrac{MD}{DA}dfrac{NC}{CB}
Hướng dẫn : Kéo dài các tia DA, CB cắt nhau tại E (h.3), áp dụng định lí Ta - let trong tam giác và tính chất của tỉ lệ thức để chứng minh
Đọc tiếp
Cho hình thang ABCD có AB //CD và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
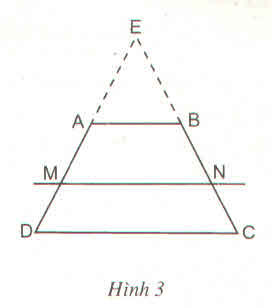
Chứng minh rằng :
a) \(\dfrac{MA}{AD}=\dfrac{NB}{BC}\)
b) \(\dfrac{MA}{MD}=\dfrac{NB}{NC}\)
c) \(\dfrac{MD}{DA}=\dfrac{NC}{CB}\)
Hướng dẫn : Kéo dài các tia DA, CB cắt nhau tại E (h.3), áp dụng định lí Ta - let trong tam giác và tính chất của tỉ lệ thức để chứng minh
Cho hình thang ABCD (AB // CD) và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD , BC theo thứ tự tại M, N. Chứng minh rằng: a) MA NB AD BC = b) MA NB MD NC = c) MD NC DA CB = Hướng dẫn: Kéo dài các tia DA và CB cắt nhau tại E, áp dụng định lý Ta – lét trong tam giác và tính chất tỉ lệ thức để chứng minh
giúp mik với thanks nhiều nha:))
Lấy P là một điểm thuộc cạnh AD của hình bình hành ABCD sao cho AP = \(\dfrac{1}{5}\)AD. Gọi Q là giao điểm của AC và BP. Chứng minh: AQ=\(\dfrac{1}{6}\)AC
Bài 10: Cho ∆ABC cân tại A. Đường vuông góc với BC tại B cắt đường vuông góc với AC tại Có D. Vẽ BE vuông góc với CD tại E. gọi M là giao điểm của AD và BE. Vē EN vuông góc với BD tại N. a) Chứng minh DE/DC = DM/DA b) Chứng minh MN//AB. c) Chứng minh ME = MB
6*. Cho tam giác ABC có AM là trung tuyến và điểm E thuộc đoạn thẳng MC. Qua E kẻ đường thẳng song song với
AC, cắt AB ở D và cắt AM ở K. Qua E kẻ đường thẳng song song với AB, cắt AC ở F. Chứng minh CFDK.
7*. Cho tam giác ABC nhọn, M là trung điểm của BC và H là trực tâm. Đường thẳng qua H và vuông góc với MH cắt
AB và AC theo thứ tự ở I và K. Qua C kẻ đường thẳng song song với IK, cắt AH và AB theo thứ tự ở N và D. Chứng
minh:
a) NCND . b) HIHK
8*. Cho hình bình hành ABCD. Gọi E là một điểm...
Đọc tiếp
6*. Cho tam giác ABC có AM là trung tuyến và điểm E thuộc đoạn thẳng MC. Qua E kẻ đường thẳng song song với
AC, cắt AB ở D và cắt AM ở K. Qua E kẻ đường thẳng song song với AB, cắt AC ở F. Chứng minh CF=DK.
7*. Cho tam giác ABC nhọn, M là trung điểm của BC và H là trực tâm. Đường thẳng qua H và vuông góc với MH cắt
AB và AC theo thứ tự ở I và K. Qua C kẻ đường thẳng song song với IK, cắt AH và AB theo thứ tự ở N và D. Chứng
minh:
a) NC=ND . b) HI=HK
8*. Cho hình bình hành ABCD. Gọi E là một điểm bất kỳ trên cạnh AB. Qua E kẻ đường thẳng song song với AC cắt
BC ở F và kẻ đường thẳng song song với BD cắt AD ở H. Đường thẳng kẻ qua F song song với BD cắt CD ở G. Chứng
minh AH.CD=AD.CG.
cho hình chữ nhật ABCD. M là hình chiếu của A trên BD.
a) Chứng minh tam giác ABD đồng dạng với tam giác MAD
b) Nếu AB=8cm, AD=6cm, tính đoạn DM.
c) đường thẳng AM cắt các đường thẳng DC và BC thứ tự tại N và P. Chứng minh AM^2 = MN.MP
d) Lấy điểm E trên cạnh AB,F trên cạnh BC, EF cắt BD ở K. Chứng minh AB/BE+BC/BF=BD/BK










