Hình học lớp 7
Các câu hỏi tương tự
8.Cho hình 11, biết rằng AB AC. Trong các kết luận sau kết luận nào đúng ? Tại sao?
a) HB HC
b) HB HC
c) HB HC
Hướng dẫn:
Vì AB AC (gt) mà AB, AC là hai đường xiên có hai hình chiếu tương ứng là HB và HC nên HB HC
9.Để tập bơi nâng dần khoảng cách, hàng ngày bạn Nam xuất phát từ M, ngày thứ nhất bạn bơi đến A, ngày thứ hai bạn bơi đến B, ngày thứ ba bạn bơi đến C..(hình 12)
Hỏi rằng bạn Nam tập bơi như thế có đúng mục đích đề ra hay không ( ngày hôm sau có bơi xa hơn ngày hôm t...
Đọc tiếp
8.Cho hình 11, biết rằng AB < AC. Trong các kết luận sau kết luận nào đúng ? Tại sao?
a) HB = HC
b) HB > HC
c) HB < HC

Hướng dẫn:
Vì AB < AC (gt) mà AB, AC là hai đường xiên có hai hình chiếu tương ứng là HB và HC nên HB > HC
9.Để tập bơi nâng dần khoảng cách, hàng ngày bạn Nam xuất phát từ M, ngày thứ nhất bạn bơi đến A, ngày thứ hai bạn bơi đến B, ngày thứ ba bạn bơi đến C..(hình 12)
Hỏi rằng bạn Nam tập bơi như thế có đúng mục đích đề ra hay không ( ngày hôm sau có bơi xa hơn ngày hôm trước hay không? Vì sao?
Hướng dẫn:
Theo hình vẽ các điểm A, B, C, D nằm trên một đường thẳng d và điểm M nằm ngoài đường thẳng đó. MA là đường vuông góc kẻ từ M đến đường thẳng d. Các đoạn thẳng MB, MC, MD là các đường xiên kẻ từ M lần lượt đến B, C và D
Ta có AB, AC, AD lần lượt là hình chiếu của MB, MC, MD xuống d. Ta có ngay AD >AC > AB suy ra
MD > MC >MB > MA
Điều đó có nghĩa là ngày hôm sau bạn Nam bơi đươci xa hơn ngày hôm trước, tức là bạn Nam tập đúng mục đích đề ra
Chứng minh rằng trong một tam giác cân, độ dài đoạn thẳng nối đỉnh đối diện với đáy và một điểm bất kỳ của cạnh đáy nhỏ hơn hoặc bằng độ dài của cạnh bên.
Hướng dẫn:
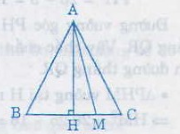
Giả sử ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC
3 bài tập SGK 7 trang 59
Cho tam giác ABC vuông tại A. Đường cao AH , Biết HC-HB=AB, Tính góc ACB
Cho tam giác ABC nhọn có AD và BE là hai đường cao cắt nhau tại H.
a, Cho góc ABC> góc ACB. C/minh HC >HB
b, Vẽ HF vuông AB tại F. c/m 3 điểm C, H, F thẳng hàng
c, c/m AB +AC >2AD
d, C/m HA +HB+AC <2/3 <AB +AC+BC
Cho tam giác ABC nhọn có góc B=2C,gọi H là hình chiếu vuông góc của A trên bc. Trên tia đối của tia BA lấy điểm E sao cho BE=BH, đường thẳng EH cắt AC ở D. CM:
1) HC > HB
2) tam giác HDC cân và D là trung điểm của AC
3) AB2+HC2=AC2+HB2 và BC2+AB2-AC2 =2BH . BC
4)AE=HC
cho tam giác abc vuông tại a đường cao ah ,ab=6cm ,bc=10cm.tính ah,hb,hc
Cho tam giác ABC vuông tại A có đường cao AH.
Biết AH= 4cm ; HB = 2cm ; HC= 8cm
a) tính độ dài các cạnh AB,AC
b) chứng minh góc B > góc C
Cho tam igác nhọn ABC trực tâm H. Chứng minh HA + HB + HC< 2/3( AB+AC+BC)
Cho tam giac ABC vuong tai A, goc C=30do. Duong cao AH. Tren canh HC lay diem D sao cho HD=HB. Tu C keo CE vuong goc AD. Cm. a, Tam giac ABD deu. b, EH song song AC
Cho ABC CÓ\(\widehat{A}\)=900 VẼ AH\( \perp\)BC,H\(\in\)BC
a) AB=6cm,AC=8cm tính BC
b) Cho HB=4cm, HC=9cm tính AH












