Gọi R là bán kính của đường tròn (C)
(C) và C1 tiếp xúc ngoài với nhau, cho ta:
MF1 = R1+ R (1)
(C) và C2 tiếp xúc ngoài với nhau, cho ta:
MF2 = R2 – R (2)
Từ (1) VÀ (2) ta được
MF1 + MF2 = R1+ R2= R không đổi
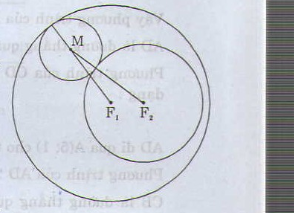
Điểm M có tổng các khoảng cách MF1 + MF2 đến hai điểm cố định F1 và F2 bằng một độ dài không đổi R1+ R2
Vậy tập hợp điểm M là đường elip, có các tiêu điểm F1 và F2 và có tiêu cực :
F1 .F2 = R1+ R2




