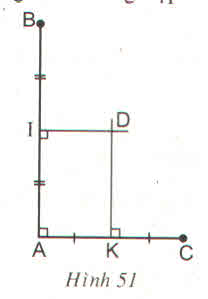
a: Ta có: O là tâm đường tròn ngoại tiếp ΔABC
nên OA=OB=OC
Ta có: ΔBAC vuông tại A
nên A nằm trên đường tròn đường kính BC
=>O thuộc BC
b: Sửa đề: \(\widehat{AOB}=2\cdot\widehat{BCA}=2\cdot\widehat{BDA}\)
Xét (O) có
góc BCA là góc nội tiếp chắn cung BA
góc BDA là góc nội tiếp chắn cung BA
Do đó: \(\widehat{BCA}=\widehat{BDA}\left(1\right)\)
Xét ΔOAC có OA=OC
nên ΔOAC cân tại O
=>\(\widehat{OAC}=\widehat{OCA}\)
=>\(\widehat{AOB}=2\cdot\widehat{BCA}\)(2)
Từ (1) và (2) suy ra \(\widehat{AOB}=2\cdot\widehat{BCA}=2\cdot\widehat{BDA}\)
c: Xét (O) có
góc AOD là góc ở tâm chắn cung AD
góc ACD là góc nội tiếp chắn cung AD
Do đó: \(\widehat{AOD}=2\cdot\widehat{ACD}\)