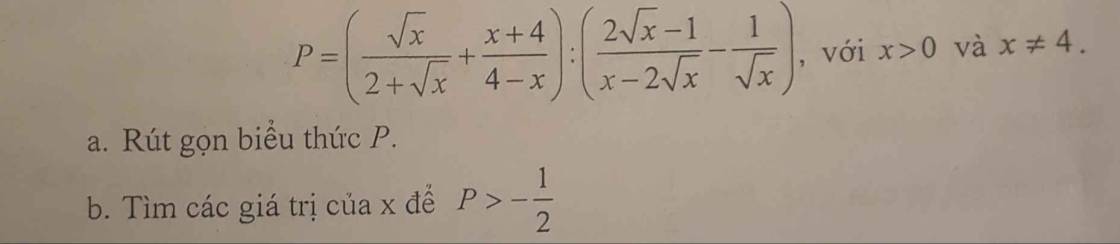a: \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}+2}-\dfrac{x+4}{x-4}\right):\dfrac{2\sqrt{x}-1-\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)-x-4}{x-4}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\sqrt{x}+1}\)
\(=\dfrac{-2\sqrt{x}-4}{x-4}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\sqrt{x}+1}\)
\(=-\dfrac{2\sqrt{x}}{\sqrt{x}+1}\)
b: P>-1/2
=>\(P+\dfrac{1}{2}>0\)
=>\(-\dfrac{2\sqrt{x}}{\sqrt{x}+1}+\dfrac{1}{2}>0\)
=>\(\dfrac{-4\sqrt{x}+\sqrt{x}+1}{2\left(\sqrt{x}+1\right)}>0\)
=>\(-3\sqrt{x}+1>0\)
=>\(-3\sqrt{x}>-1\)
=>\(\sqrt{x}< \dfrac{1}{3}\)
=>\(0< x< \dfrac{1}{9}\)
Đúng 1
Bình luận (0)
