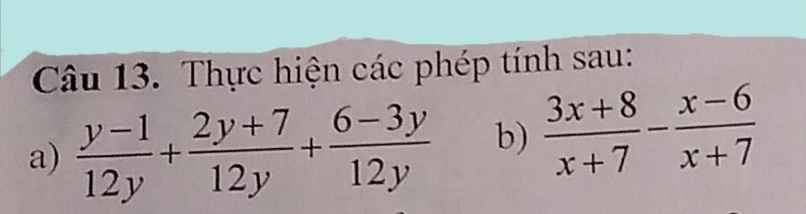e: ĐKXĐ: \(a\notin\left\{-1;1\right\}\)
\(\dfrac{a}{a+1}-\dfrac{a}{a-1}-\dfrac{2a^2}{1-a^2}\)
\(=\dfrac{a}{a+1}-\dfrac{a}{a-1}+\dfrac{2a^2}{\left(a-1\right)\left(a+1\right)}\)
\(=\dfrac{a\left(a-1\right)-a\left(a+1\right)+2a^2}{\left(a+1\right)\left(a-1\right)}\)
\(=\dfrac{a^2-a-a^2-a+2a^2}{\left(a+1\right)\left(a-1\right)}=-\dfrac{2a}{a^2-1}\)
g: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\dfrac{4}{x+2}+\dfrac{2}{x-2}+\dfrac{5x-6}{4-x^2}\)
\(=\dfrac{4}{x+2}+\dfrac{2}{x-2}-\dfrac{5x-6}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{4\left(x-2\right)+2\left(x+2\right)-5x+6}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{4x-8+2x+4-5x+6}{\left(x-2\right)\left(x+2\right)}=\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}=\dfrac{1}{x-2}\)
h: ĐKXĐ: x<>1
\(\dfrac{x^2+2}{x^3-1}+\dfrac{2}{x^2+x+1}-\dfrac{1}{x-1}\)
\(=\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{2}{x^2+x+1}-\dfrac{1}{x-1}\)
\(=\dfrac{x^2+2+2\left(x-1\right)-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{-x+1+2x-2}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{1}{x^2+x+1}\)
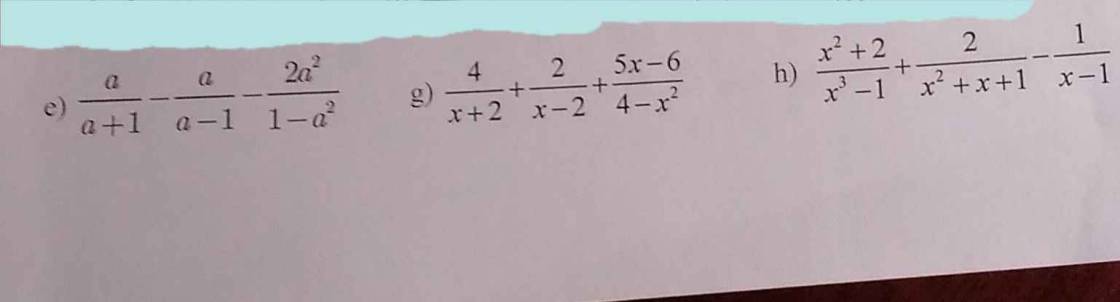
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
