a. ĐKXĐ: \(x\ge4\)
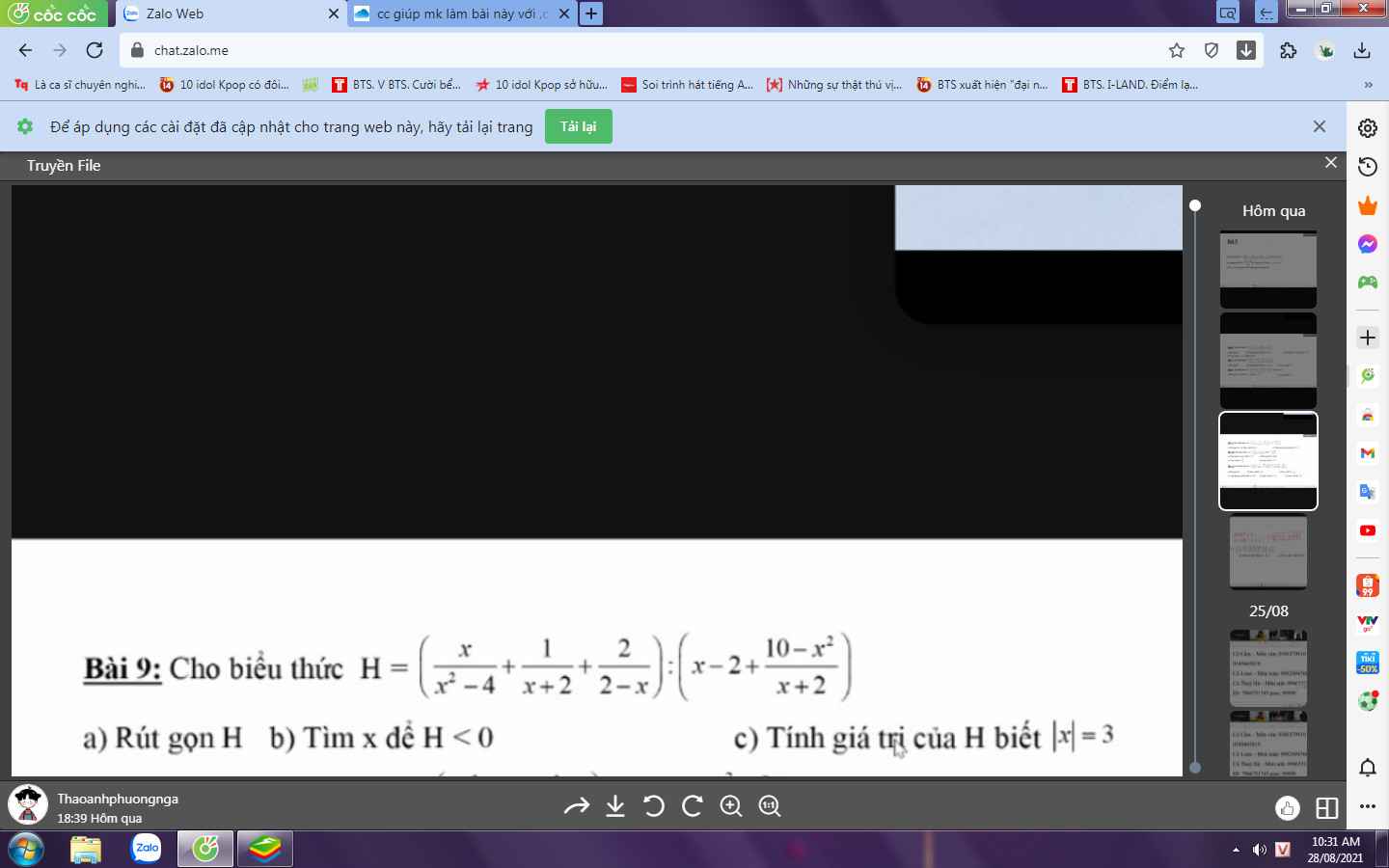
\(F=\left(\dfrac{2+x}{2-x}-\dfrac{4x^2}{x^2-4}-\dfrac{2-x}{2+x}\right):\dfrac{x^2-3x}{2x^2-x^3}\)
\(=\left(\dfrac{\left(2+x\right)\left(2+x\right)}{\left(2-x\right)\left(2+x\right)}+\dfrac{4x^2}{\left(2-x\right)\left(2+x\right)}-\dfrac{\left(2-x\right)\left(2-x\right)}{\left(2-x\right)\left(2+x\right)}\right):\dfrac{x\left(x-3\right)}{x^2\left(2-x\right)}\)
\(=\dfrac{4+4x+x^2+4x^2-4+4x-x^2}{\left(2-x\right)\left(2+x\right)}.\dfrac{x^2\left(2-x\right)}{x\left(x-3\right)}\)
\(=\dfrac{4x^2+8x}{\left(2-x\right)\left(2+x\right)}.\dfrac{x^2\left(2-x\right)}{x\left(x-3\right)}=\dfrac{4x\left(x+2\right)x^2\left(2-x\right)}{\left(x+2\right)\left(2-x\right)x\left(x-3\right)}=\dfrac{4x^2}{x-3}\)
b. Ta có \(\left|x-5\right|=2\) \(\Leftrightarrow\left[{}\begin{matrix}x-5=2\\5-x=2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=3\end{matrix}\right.\)
* Với \(x=7\), ta có biểu thức \(F=\dfrac{4.7^2}{7-3}=\dfrac{196}{4}=49\)
* Với \(x=3\), ta có biểu thức \(F=\dfrac{4.3^2}{3-3}=\dfrac{36}{0}\), lúc này biểu thức không xác định
c. \(F>0\Leftrightarrow\dfrac{4x^2}{x-3}>0\), vì \(4x^2\ge0\forall x\) nên để \(\dfrac{4x^2}{x-3}>0\) thì \(\left\{{}\begin{matrix}4x^2>0\\x-3>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>0\\x>3\end{matrix}\right.\) \(\Leftrightarrow x>3\)
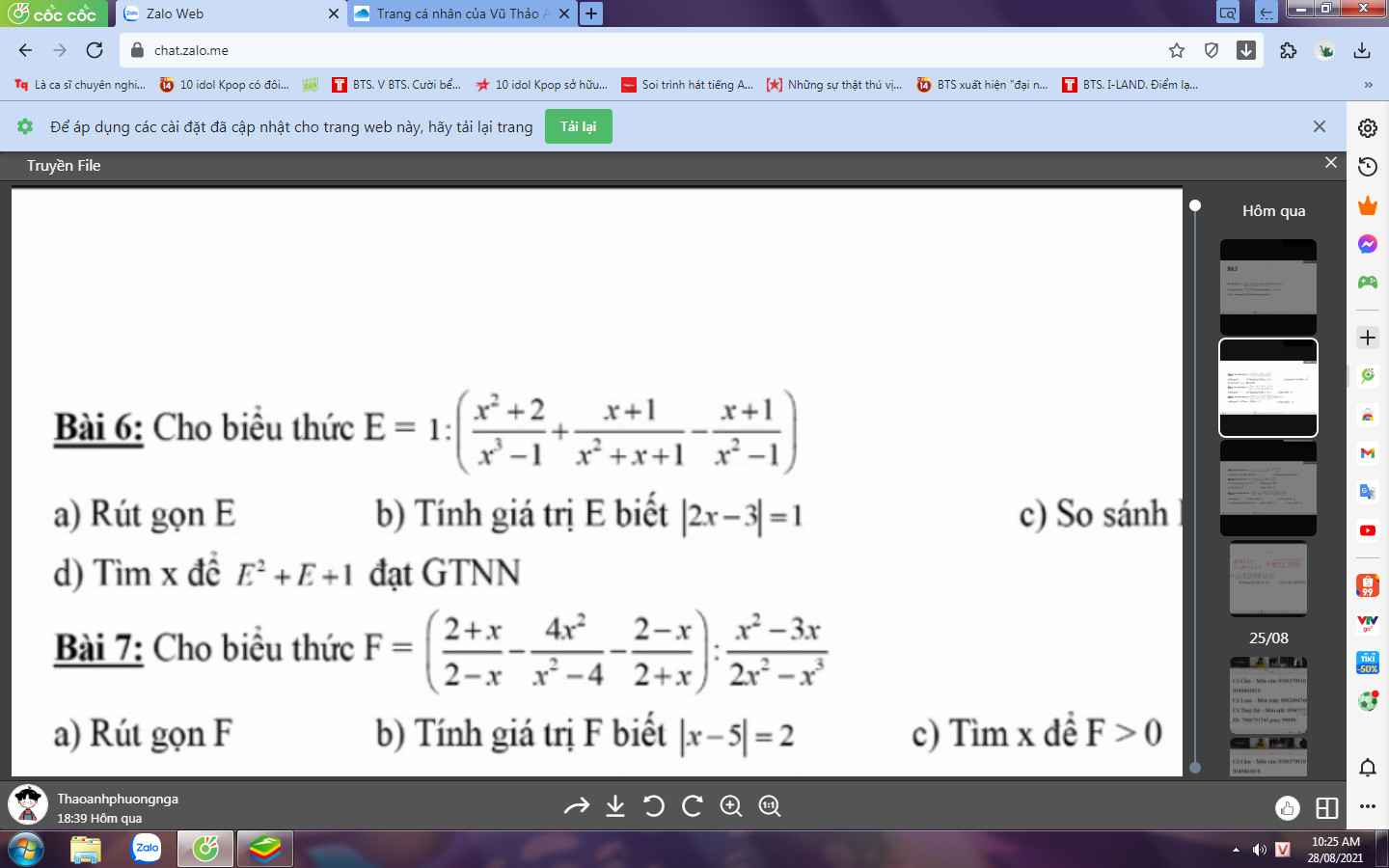
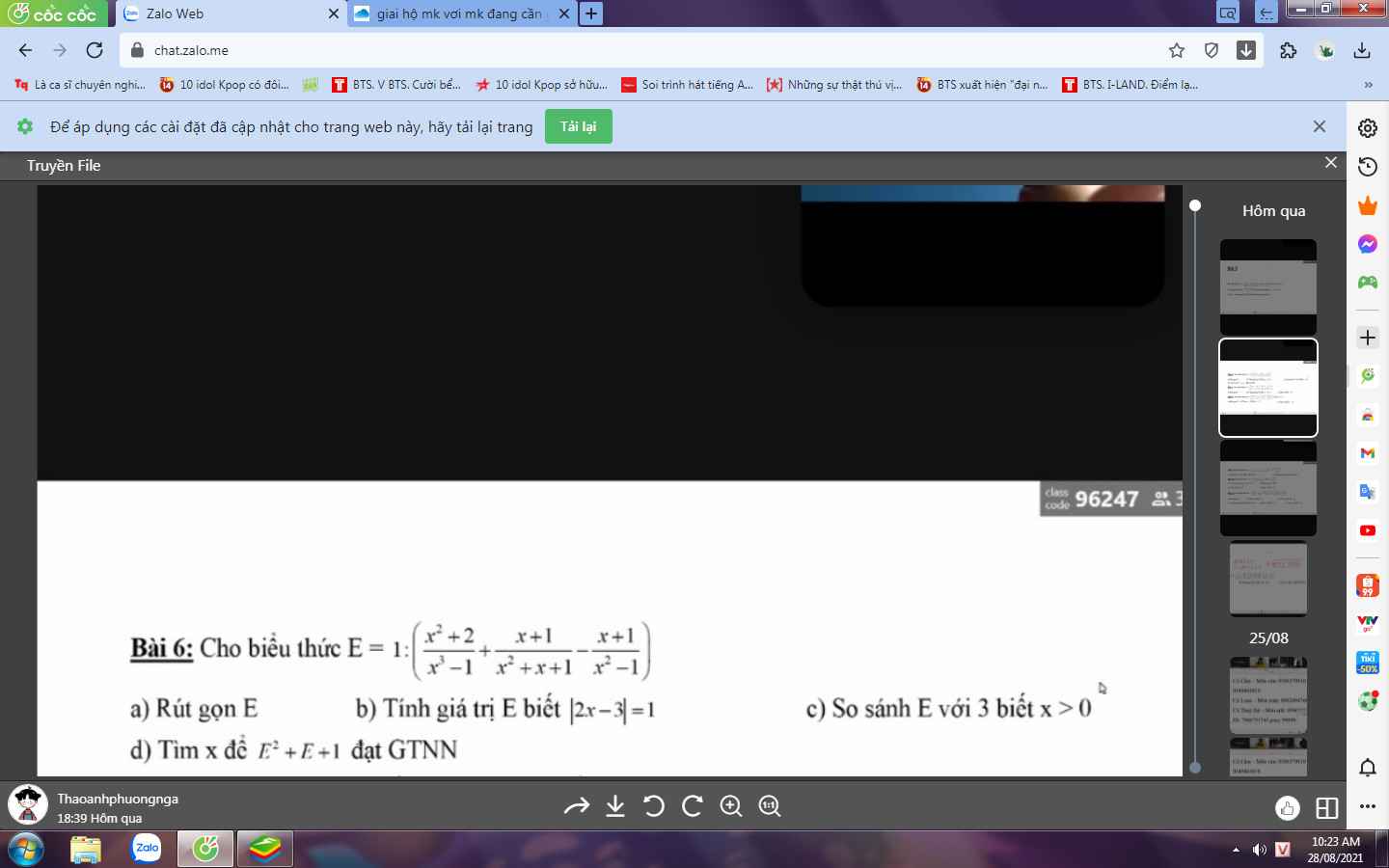
Bài 6:
a: Ta có: \(E=1:\left(\dfrac{x^2+2}{x^3-1}-\dfrac{x+1}{x^2+x+1}-\dfrac{x+1}{x^2-1}\right)\)
\(=1:\left(\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{x^2-1}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\right)\)
\(=1:\dfrac{x^2+2-x^2+1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=1\cdot\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{-x^2-x+2}\)
\(=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{-\left(x^2+x-2\right)}\)
\(=\dfrac{-\left(x-1\right)\left(x^2+x+1\right)}{\left(x+2\right)\left(x-1\right)}\)
\(=\dfrac{-x^2-x-1}{x+2}\)
b: Ta có: |2x-3|=1
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=1\\2x-3=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=4\\2x=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=1\left(loại\right)\end{matrix}\right.\)
Thay x=2 vào E, ta được:
\(E=\dfrac{-2^2-2-1}{2+2}=\dfrac{-7}{4}\)
Bài 7:
a: Ta có: \(F=\left(\dfrac{2+x}{2-x}-\dfrac{4x^2}{x^2-4}-\dfrac{2-x}{2+x}\right):\dfrac{x^2-3x}{2x^2-x^3}\)
\(=\left(\dfrac{-\left(x+2\right)}{x-2}-\dfrac{4x^2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x-2}{x+2}\right):\dfrac{x^2-3x}{2x^2-x^3}\)
\(=\dfrac{-\left(x+2\right)^2-4x^2+\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}:\dfrac{x^2-3x}{2x^2-x^3}\)
\(=\dfrac{-x^2-4x-4-4x^2+x^2-4x+4}{\left(x-2\right)\left(x+2\right)}:\dfrac{x\left(x-3\right)}{x^2\left(2-x\right)}\)
\(=\dfrac{-8x}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{-x\left(x-2\right)}{x-3}\)
\(=\dfrac{8x^2}{\left(x+2\right)\left(x-3\right)}\)






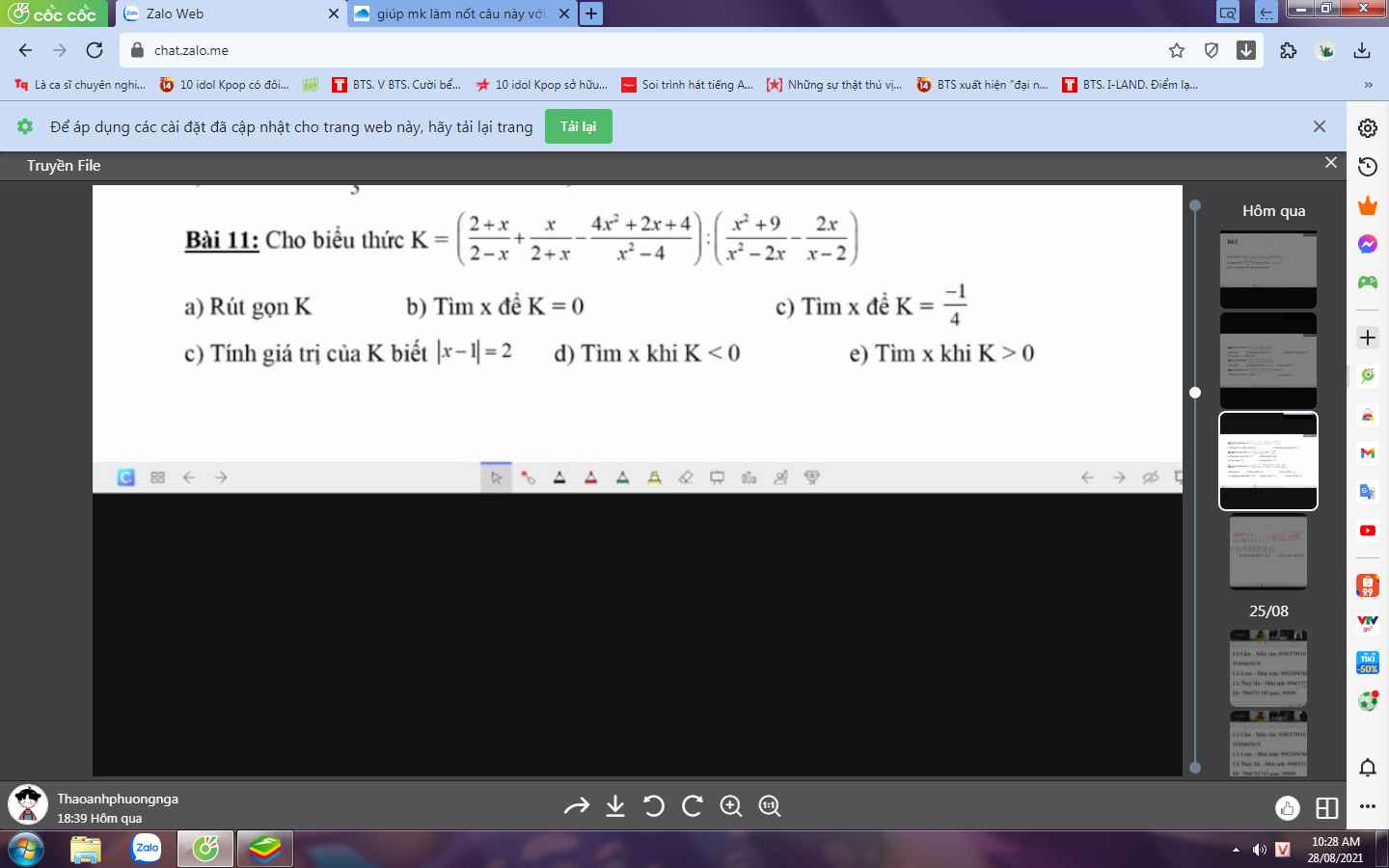
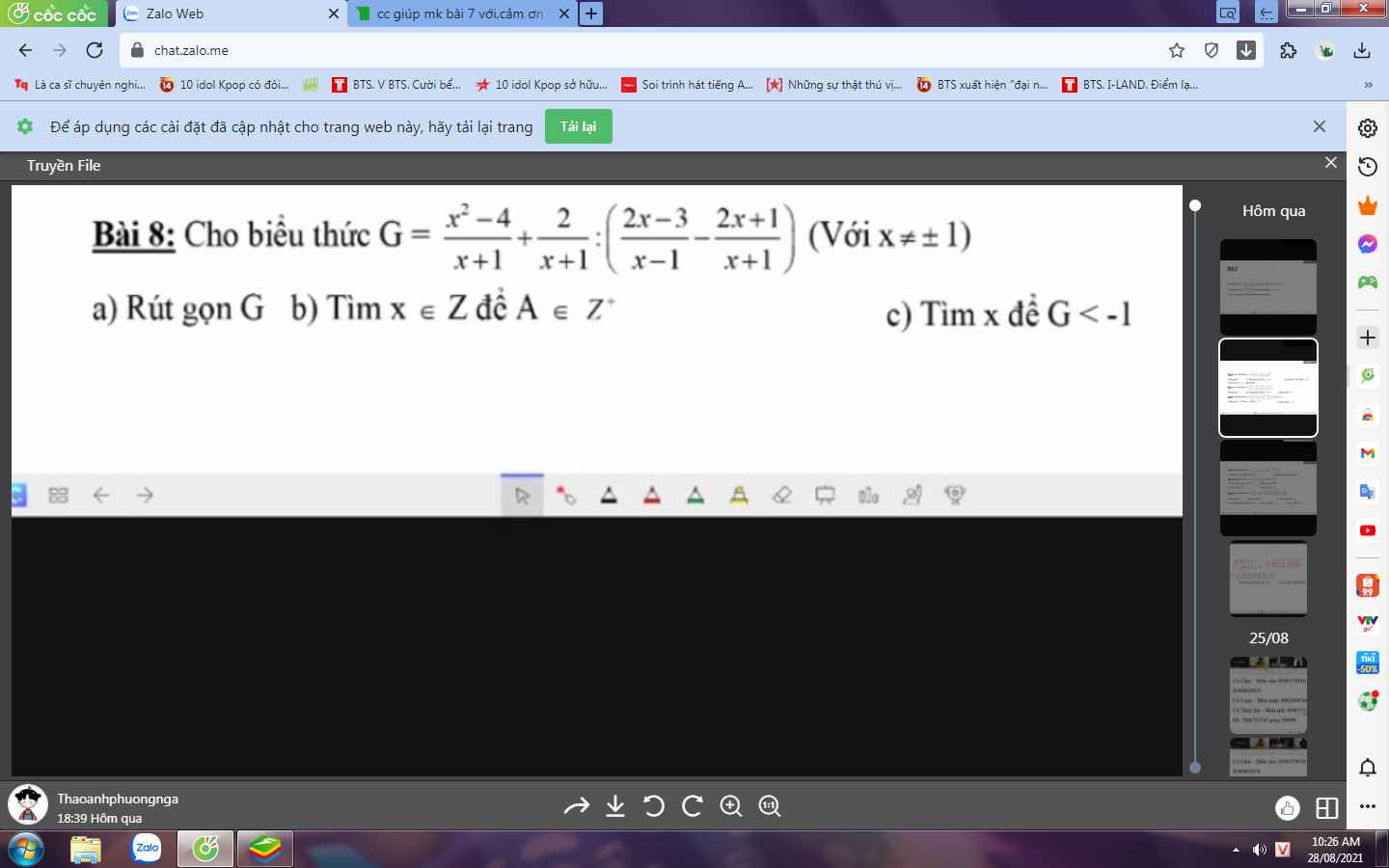
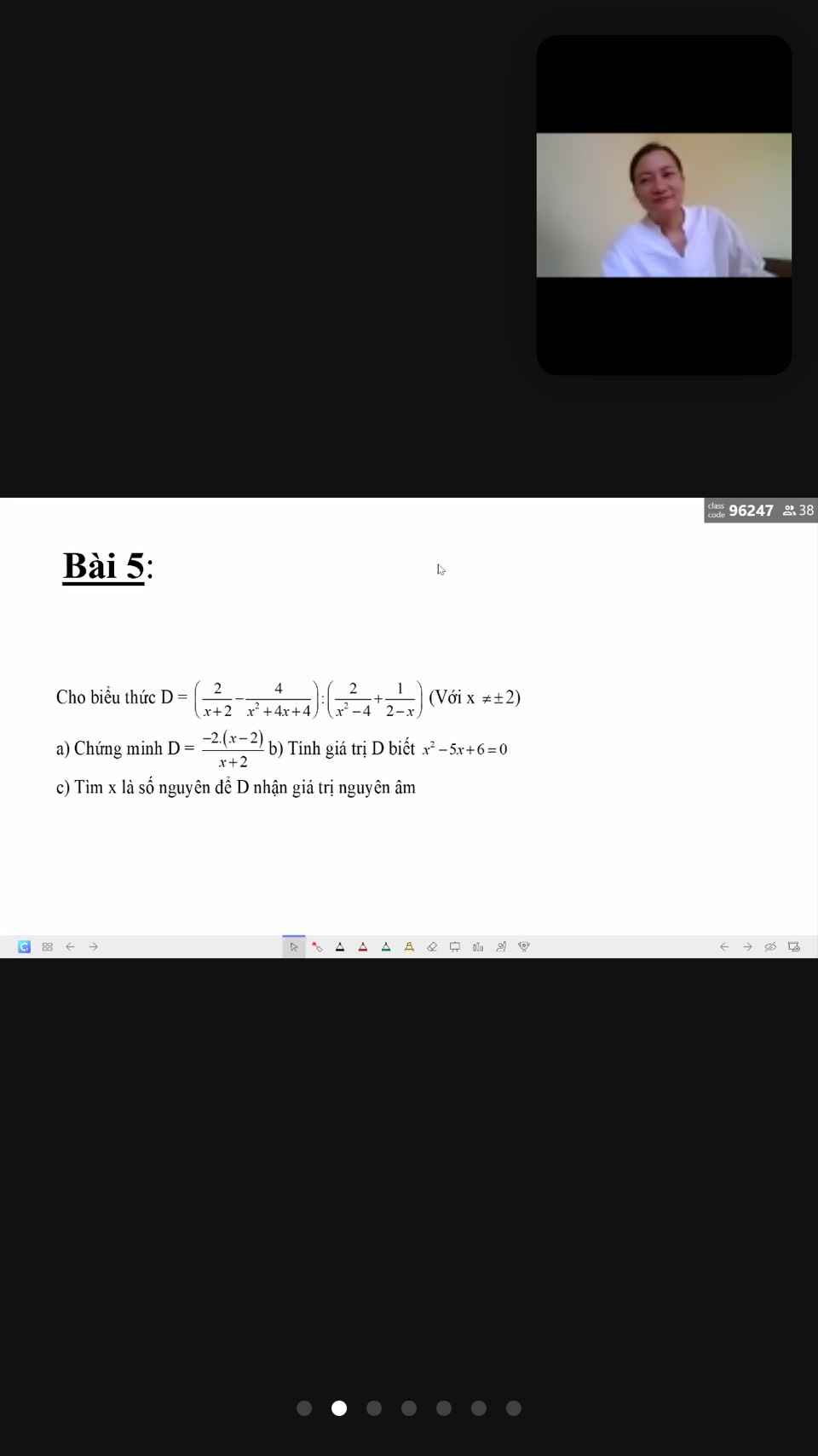 giúp mk làm nốt mấy câu này với,cảm ơn trước nhá
giúp mk làm nốt mấy câu này với,cảm ơn trước nhá