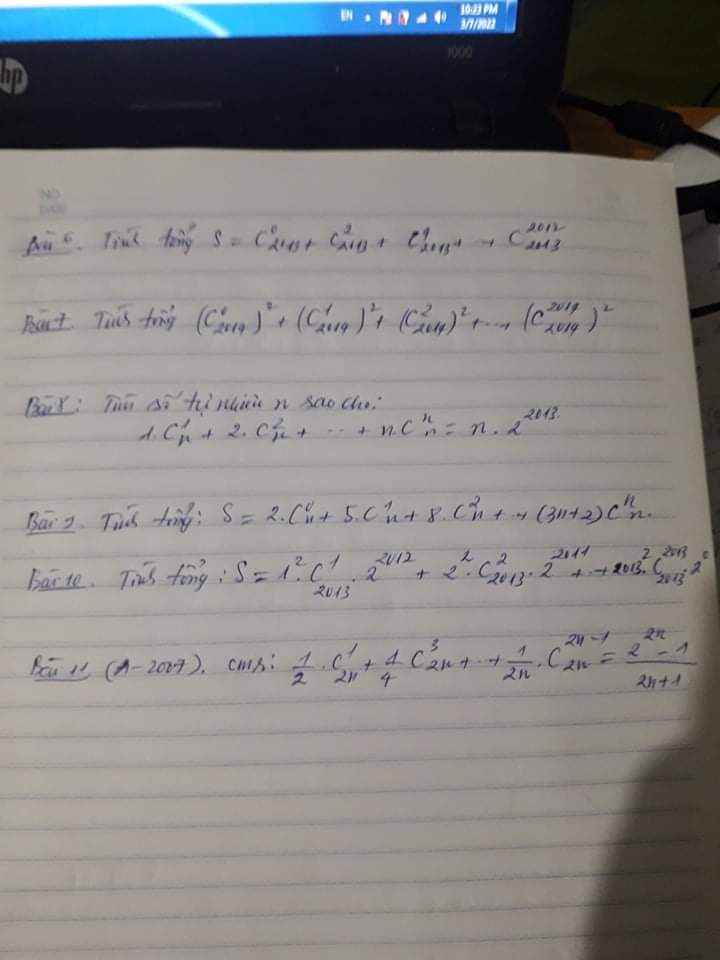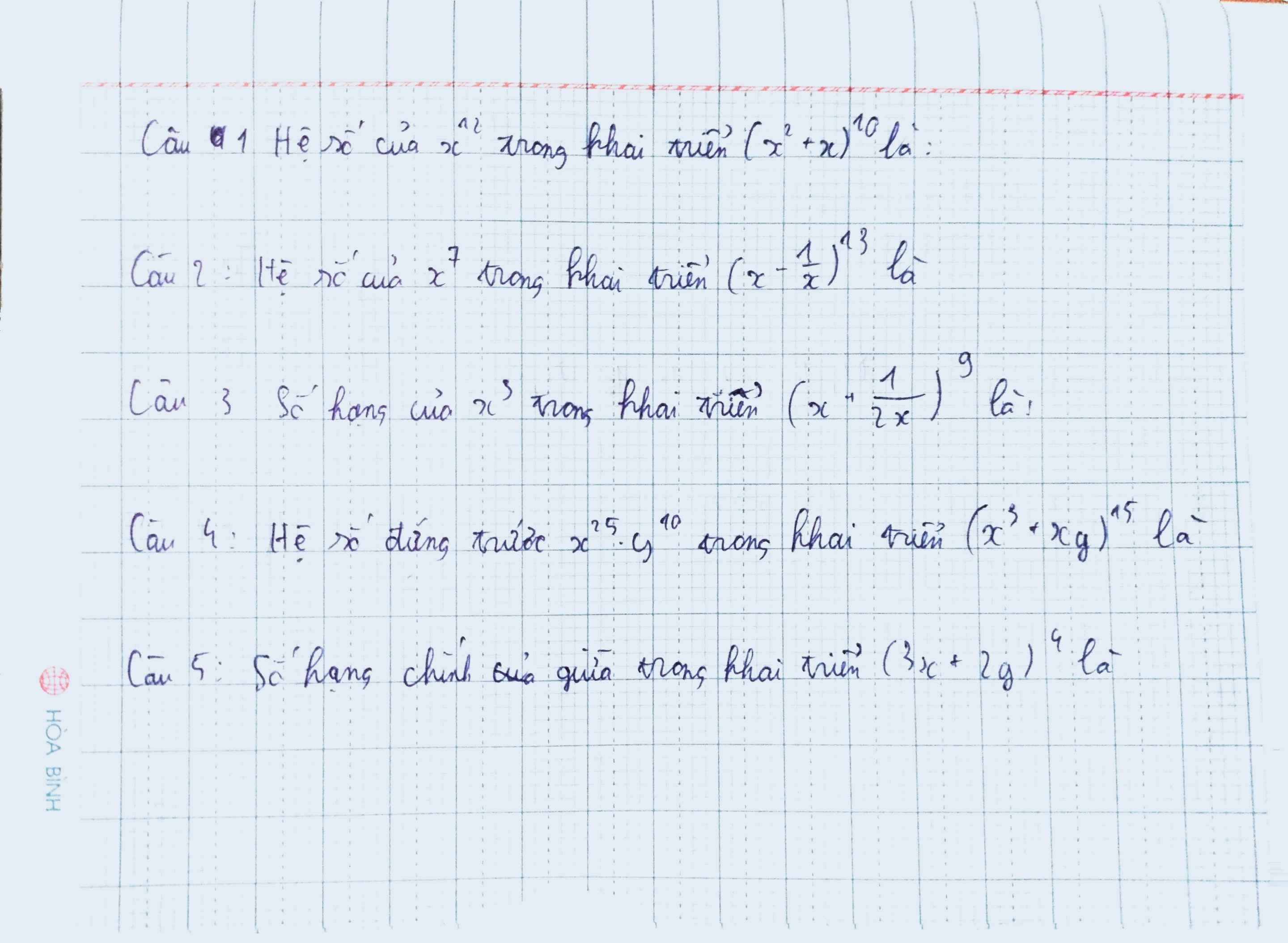7.
Bài toán: từ 1 nhóm có 2n người, bao gồm đúng n nam và n nữa, hỏi có bao nhiêu cách chọn ra n người khác nhau.
- Cách chọn thứ nhất: chọn n người từ 2n người, có \(C_{2n}^n\) cách
- Cách chọn thứ 2: giả sử trong n người được chọn, có k nam và n-k nữ (với k từ 0 tới n)
Chọn k nam từ n nam: có \(C_n^k\) cách, chọn n-k nữ từ n nữ, có \(C_n^{n-k}=C_n^k\) cách
\(\Rightarrow\) có \(\sum\limits^n_{k=0}C_n^k.C_n^k=\sum\limits^n_{k=0}\left(C_n^k\right)^2\)
Do 2 cách chọn đều có kết quả giống nhau, suy ra:
\(C_{2n}^n=\sum\limits^n_{k=0}\left(C_n^k\right)^2=\left(C_n^0\right)^2+\left(C_n^1\right)^2+...+\left(C_n^n\right)^2\)
Thay \(n=2014\Rightarrow\left(C_{2014}^0\right)^2+\left(C_{2014}^1\right)^2+...+\left(C_{2014}^{2014}\right)^2=C_{4028}^{2014}\)
8.
Xét khai triển:
\(\left(1+x\right)^n=C_n^0+C_n^1x+C_n^2x^2+...+C_n^nx^n\)
Đạo hàm 2 vế:
\(n\left(1+x\right)^{n-1}=C_n^1+2C_n^2x+...+nC_n^nx^{n-1}\)
Thay \(x=1\) vào đẳng thức trên ta được:
\(n.2^{n-1}=C_n^1+2C_n^2+3C_n^3+...+nC_n^n\)
\(\Rightarrow n.2^{n-1}=n.2^{2013}\)
\(\Rightarrow n-1=2013\)
\(\Rightarrow n=2014\)
Câu 8 nếu ko sử dụng đạo hàm thì còn cách khác như sau:
Ta có:
\(kC_n^k=k.\dfrac{n!}{k!\left(n-k\right)!}=\dfrac{n!}{\left(k-1\right)!\left(n-k!\right)}=n.\dfrac{\left(n-1\right)!}{\left(k-1\right)!\left[\left(n-1\right)-\left(k-1\right)\right]!}=n.C_{n-1}^{k-1}\)
Từ đó ta có:
\(1.C_n^1+2C_n^2+3C_n^3+...+nC_n^n=nC_{n-1}^0+nC_{n-1}^1+...+nC_{n-1}^{n-1}\)
\(=n\left(C_{n-1}^0+C_{n-1}^1+...+C_{n-1}^{n-1}\right)\)
\(=n.2^{n-1}\)
\(\Rightarrow n.2^{n-1}=n.2^{2013}\Rightarrow n=2014\)
9.
Tương tự câu 8, ta chứng minh được: \(kC_n^k=nC_{n-1}^{k-1}\Rightarrow\sum kC_n^k=n.2^{n-1}\)
Do đó:
\(S=\left(3.0+2\right)C_n^0+\left(3.1+2\right)C_n^1+...+\left(3n+2\right)C_n^n\)
\(=\left(3.1C_n^1+3.2C_n^2+...+3.nC_n^n\right)+\left(2C_n^0+2C_n^1+...+2C_n^n\right)\)
\(=3\left(1.C_n^1+2.C_n^2+...+nC_n^n\right)+2\left(C_n^0+C_n^1+...+C_n^n\right)\)
\(=3.n.2^{n-1}+2.2^n\)
\(=\left(3n+4\right).2^{n-1}\)