ta có : \(\dfrac{\left(n+3\right)!}{n!}=\dfrac{1.2.3...n.\left(n+1\right)\left(n+2\right)\left(n+3\right)}{1.2.3...n}\)
\(\left(n+1\right)\left(n+2\right)\left(n+3\right)\)
ta có : \(\dfrac{\left(n+3\right)!}{n!}=\dfrac{1.2.3...n.\left(n+1\right)\left(n+2\right)\left(n+3\right)}{1.2.3...n}\)
\(\left(n+1\right)\left(n+2\right)\left(n+3\right)\)
mọi người giải thích cho e chỗ hệ số ở VP với, em chưa hiểu chổ đó em cảm ơn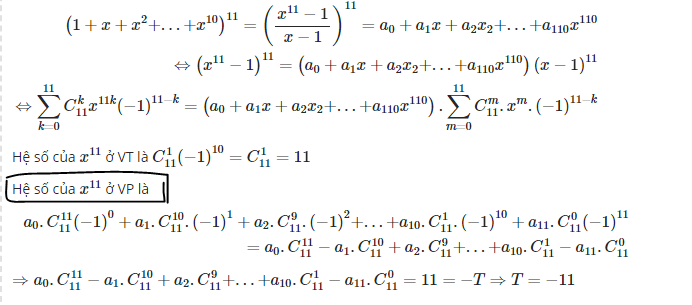
Các bạn giúp mình khai triển chi tiết biểu thức (a+ b)n theo nhị thức niuton đi.
Để cụ thể hơn các bạn vui lòng khai triển chi tiết biểu thức ( \(\sqrt{3}+\sqrt[3]{30}\))6 (đến khi ra kết quả luôn nha) theo nhị thức niuton hộ mình nha
Các bạn giúp mình khai triển chi tiết biểu thức (a+ b)n theo nhị thức niuton đi.
Để cụ thể hơn các bạn vui lòng khai triển chi tiết biểu thức \(\left(\sqrt{3}+\sqrt[3]{30}\right)^6\) (đến khi ra kết quả luôn nha) theo nhị thức niuton hộ mình nha
khai triển của biểu thức (x^2+x+1)^2018 được viết thành a0+a1x+a2x^2+…+a4036x^4036. Tổng S=a0-a2+a4-a6+…-a4034+a4036 bằng
A. -1
B. 0
C. 2^1009
D. -2^1009
giải chi tiết dễ hiểu!
Các bạn giúp mình khai triển chi tiết biểu thức (a+ b)n theo nhị thức niuton đi.
Để cụ thể hơn các bạn vui lòng khai triển chi tiết biểu thức \(\left(\sqrt{3}+\sqrt[3]{30}\right)^6\) (tính ra kết quả hộ mình luôn nha) theo nhị thức niuton hộ mình nha
Bài 2 a) Tìm hệ số của x^3 trong khai triển của (x+2/x^2)^6
b) Tìm hệ số của x^7 trong khai triển (3-2x)^15
c) Tìm số hạng không chứa x trong khai triển (2x-1/x^2)^6
(^: là mũ nhé mn,bài này mình vừa học ở trường nhưng chưa hiểu mn giúp chi tiết,cảm ơn mn ^•^)
Tìm hệ số của số hạng chứa x20 trong khi khai triển nhị thức \(\left(\dfrac{1}{x^3}+x^2\right)^n\)
Biết: \(C^{n+1}_{2n+1}+C^{n+2}_{2n+1}+C^{n+3}_{2n+1}+...+C^{2n}_{2n+1}=2^{100}-1\)
Ai giải giùm bài này với !!!
Các bạn giúp mình khai triển chi tiết biểu thức (a\(+\) b)n theo nhị thức niuton đi.
Để cụ thể hơn các bạn vui lòng khai triển chi tiết biểu thức (\(\sqrt{3}\) \(+\) \(\sqrt[3]{30}\) )6 theo nhị thức niuton hộ mình nha
Giúp em bài này với ạ